Пример.

Случайная величина.

Пример.

Клиентами некоторого банка являются: государственные организации, коммерческие организации, физические лица. На их долю приходятся следующие объемы заимствованных средств: государственные организации - 5%,коммерческие организации - 15%,физические лица – остальной объем кредита. Определить общую вероятность невозврата кредита, если вероятность невозврата кредита государственной организацией составляет 0,001,коммерческой организацией - 0,01,физическими лицами - 0,1.

Обозначим:

событиеА –не возврат кредита, Р(А) –вероятность события А.

Н₁ –не возврат кредита государственной организацией

Н₂ –не возврат кредита коммерческой организацией

Н₃ –не возврат кредита физическими лицами

р(Н₁)=5%, р(Н₂)=15%, р(Н₃)=80%, р(А / Н₁ ) =0,001 , р(А / Н₂ )=0,01 , р(А / Н₃ )=0,1.

По формуле полной вероятности находим:

р(А)=р(Н₁)×р(А|Н₁ )+ р(Н₂)× р(А|Н₂ )+ р(Н₃)×

×р(А|Н3)=0,05×0,001+0,15×0,01+0,8×0,1=0,082.

Наряду с формулой полной вероятности, используется формула Байеса:

р(Н_i|А )=(р(Н_i )×р(А|Н_i))/р(А),

где р(А)рассчитывается по формуле полной вероятности. Формула Байеса позволяет определить вероятность осуществления гипотезы в случае если произошло событие А.

 

Часто с каждым из возможных исходов опыта можно связать некоторое число.

 

 

1) При бросании кубика с исходом опыта можно связать число, нанесённое на грань этого кубика: напримерΩ={1,2,3,4,5,6}. Число, которое выпадает при бросании кубика есть случайная величина.

2) Число часов безотказной работы лампочки.

3) Время ожидания автобуса на остановке.

Случайная величина Х есть числовая функция, определённая на множестве элементарных событий Ω. Случайная величина Х каждому элементарному событию wставит в соответствие число Х(w)=Х, w 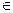Ω.

Будем обозначать:

Х, Y–случайные величины.

х, y –реализации случайной величины в данном опыте.

Случайные величины делятся на дискретные и непрерывные.