Выбор в условиях неопределенности

Выбор альтернатив

Этапы выделения альтернатив решения проблемы

1. путем анализа всех ограничений необходимо выделить множество физически реализуемых, или допустимых, альтернатив. Оптимальное или удовлетворительное решение проблемы следует искать только среди допустимых вариантов выбора;

2. из множества разумных решений следует выделить такие, которые "не хуже" других альтернатив, т.е. не менее предпочтительны с точки зре­ния степени достижения цели. Обычно для выявления таких альтернатив производится их оценка по выбранным показателям эффективности и сра­зу исключаются те решения, которые по всем показателям "не лучше" и хотя бы по одному показателю "хуже", чем некоторое допустимое решение.

 

1. Выбор альтернатив в условиях определенности.При наличие достаточной исходной информации выбор вариантов осуществляется на основание сопоставления значений целевой функции по всем сравниваемым вариантам, с учетом заданных ограничений.

2. Выбор альтернатив в условиях неопределенности.Условия неопределенности – это условия, в которых исходной информации недостаточно для определения численных значений целевой функции по каждому из сравниваемых вариантов.

 

Выбор решений в условиях неопределенности включает:

· построение матрицы эффектов и ущерба и матрицы риска

· количественную оценку вариантов.

Матрица эффектов и ущерба и матрица риска. Каждая строка матрицы (рис.4.9а) соответствует одному из вариантов намечанных решений 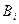, а каждый столбец – одной из ситуаций 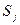которые могут возникнуть при разных значениях отсутствующей у нас информации об условиях решения проблемы или об ожидаемых результатах.

а)

Ситуация		...		...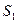
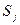
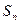
Вариант
		...		...
...	...	...	...	...	...
		...		...
...	...	...	...	...	...
		...		...

 

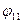
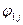
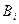
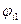
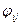
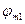
б)

Ситуация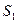
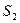
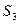
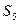
Вариант

 

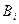
в)

Ситуация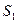
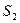
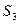
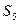
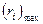
Вариант

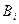
Рис. 4.9. Матрица эффектов и ущерба и матрица риска: а — матрица эффектов ущерба; б — пример заполнения матрицы эффектов и ущерба; в — пример запол­нения матрицы риска

 

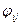С использованием информации, которой мы задались, можно опреде­лить для каждой пары соответствующие значения целевой функции . В общем случае эти значения могут быть как положительными, так и отрицательными, т.е. количественно оценивать эффект или ущерб при со­четании i-го варианта решения и j-й ситуации.

В нижнюю строку таблицы вынесены наибольшие для каждого столбца (т.е. для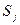) эффекты и .

Пример заполнения матрицы эффектов дан на рис. 4.9 б.

Количественной оценкой риска для каждого i-го решения при j-й си­туации принято считать разницу между максимально возможным для этой ситуации эффектом и фактическим:

.

Построенная матрица рисков имеет вид, показанный на рис. 4.9 в. Даль­нейшая процедура выбора альтернативных решений зависит от того, рас­полагаем ли мы данными о вероятности отдельных ситуаций и сколь на­дежны (достоверны) эти данные.

Количественная оценка вариантов.В случае, когда вероятности возник­новения каждой j-й ситуации известны и получены в результате обработки соответствующих статистических наблюдений, для каждой альтернативы определяют математическое ожидание значения целевой функции:

.

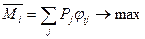При этом выбору подлежит тот альтернативный вариант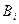, для которого математическое ожидание значения целевой функции окажется максимальным. Для этого же варианта окажется минимальным математическое ожидание риска:

.

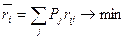В случае, когда мы не располагаем статистическими данными о Р_j, про­изводится экспертная оценка вероятности ситуации. Экспертам предлагают назвать три значения ожидаемой величины S_j , характеризующей ситуацию: оптимистическую, пессимистическую и наиболее вероятную (модальную).

Эти тройственные оценки позволяют приближенно определить мате­матическое ожидание прогнозируемой величины, т.е. средневероятное зна­чение . Если принять биномиальное распределение, то можно восполь­зоваться следующей расчетной формулой:

.

Выбор в условиях полной неопределенности

.

В тех случаях, когда дать сравнительно надежные оценки вероятности отдельных ситуаций не представляется возможным, стратегия выбора решений определя­ется опасностью риска и осторожностью лица, принимающего решение.

 

Рассмотрим стратегии выбора альтернатив.

1. Стратегия наибольшего гарантированного эффекта. Для реализации этой стратегии в каждой строке матрицы эффектов выбирается минималь­ный эффект . Лучшим считается вариант решения, для которого ми­нимальный (гарантированный) выигрыш окажется наибольшим.

Критерий, реализующий такой выбор, именуется критерием макси­мального эффекта (выигрыша), или критерием Вальда:

.

Для примера на рис.4.9 б лучшим по этому критерию является вариант B₃ , для которого R_w = 2.

2. Стратегия наименьшего возможного риска так же, как и предыдущая, ориентируется на худшую ситуацию, но не ту, которая дает наименьший эффект, а ту, которая сопряжена с наибольшим риском. В таких случаях по каждой строке матрицы риска выбирается 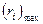, а лучшим считается вари­ант, при котором этот максимальный риск оказывается наименьшим. Кри­терий, реализующий такой выбор, именуется критерием минимального рис­ка, или критерием Сэвиджа.

.

По критерию Сэвиджа (рис. 4.9 в), лучшим является B₁, для которого R_s = 3.

3. Смешанная стратегияпредусматривает сочетание пессимизма (осторожности) и оптимизма (склонности к значительному риску), в опреде­ленно заданной пропорции. Эту стратегию реализует критерий Гурвица:

.

Для рассматриваемого примера (рис. 4.9 6) по этому критерию лучшим окажется вариант решения B₃, при этот вариант дает наибольшее значение R_H = 4.

Как видно из трех рассмотренных примеров, каждая стратегия обусло­вила свой выбор варианта. Это говорит о том, что в условиях полной нео­пределенности применение матриц эффекта и риска лишь облегчает анализ конкретной обстановки, повышает наглядность ее изучения, но не обеспе­чивает "автоматизма" в выборе решений, как при использовании вероятностных и формализованных методов.