Изменение координат вектора при изменении базиса.
Пусть в пространстве V заданы два базиса:  и
и  . Координаты вектора x в этих базисах обозначим через
. Координаты вектора x в этих базисах обозначим через  и
и  соответственно. Установим связь между координатами вектора в различных базисах. Выразим векторы первого базиса через векторы второго:
соответственно. Установим связь между координатами вектора в различных базисах. Выразим векторы первого базиса через векторы второго: 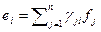 . По определению координат
. По определению координат  . Подставим вместо векторов базиса e, их выражения через векторы базиса f, получим равенство
. Подставим вместо векторов базиса e, их выражения через векторы базиса f, получим равенство . Преобразуем левую часть равенства (поменяем порядок суммирования)
. Преобразуем левую часть равенства (поменяем порядок суммирования)  . В силу единственности координат вектора выводим равенства
. В силу единственности координат вектора выводим равенства  , или в матричном виде
, или в матричном виде  , где на пересечении строки i и столбца j матрицы P стоит
, где на пересечении строки i и столбца j матрицы P стоит  . Матрица P называется матрицей перехода. Отметим, что в j столбце матрицы P стоят координаты вектора
. Матрица P называется матрицей перехода. Отметим, что в j столбце матрицы P стоят координаты вектора  в базисе f.
в базисе f.
Обозначим через  матрицу перехода от базиса e к базису f. Равенство
матрицу перехода от базиса e к базису f. Равенство  справедливо для всех векторов x. Следовательно,
справедливо для всех векторов x. Следовательно,  , или
, или  . В качестве следствия из этого равенства и условия существования обратной матрицы выводим невырожденность матрицы перехода. Обратно, пусть матрица P – невырожденная. Положим
. В качестве следствия из этого равенства и условия существования обратной матрицы выводим невырожденность матрицы перехода. Обратно, пусть матрица P – невырожденная. Положим  . Система векторов
. Система векторов  образует базис в пространстве V. Действительно, поскольку матрица P невырожденная, то к ней существует обратная матрица
образует базис в пространстве V. Действительно, поскольку матрица P невырожденная, то к ней существует обратная матрица  . Далее,
. Далее,  (выражение
(выражение  представляет собой элемент произведения матриц PT=E, стоящий на пересечении строки s и столбца i). Поскольку каждый вектор из базиса e линейно выражается через векторы системы f, то система f является полной, а т.к. система состоит из n векторов, то она является минимальной, а, значит, образует базис пространства. Матрицей перехода от базиса e к базису f является матрица P.
представляет собой элемент произведения матриц PT=E, стоящий на пересечении строки s и столбца i). Поскольку каждый вектор из базиса e линейно выражается через векторы системы f, то система f является полной, а т.к. система состоит из n векторов, то она является минимальной, а, значит, образует базис пространства. Матрицей перехода от базиса e к базису f является матрица P.
Рассмотрим систему векторов 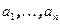 из арифметического пространства
из арифметического пространства  . Матрицу, составленную из столбцов
. Матрицу, составленную из столбцов 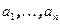 , обозначим A.
, обозначим A.
Теорема 7.8 Критерий линейной независимости системы векторов.
Система векторов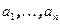 из арифметического пространства
из арифметического пространства  является линейно зависимой тогда и только тогда, когда определитель матрицы
является линейно зависимой тогда и только тогда, когда определитель матрицы  равен нулю.
равен нулю.
Доказательство. Если система 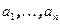 линейно зависима, то найдутся числа
линейно зависима, то найдутся числа  не все равные нулю, что
не все равные нулю, что  . Не нарушая общности можно считать, что
. Не нарушая общности можно считать, что  (иначе перенумеруем векторы), и
(иначе перенумеруем векторы), и  (иначе поделим все числа на
(иначе поделим все числа на  ). Определитель не изменится, если к первому столбцу прибавить остальные столбцы с коэффициентами
). Определитель не изменится, если к первому столбцу прибавить остальные столбцы с коэффициентами  , а определитель матрицы, содержащий нулевой столбец равен нулю. Таким образом, если система векторов линейно зависима, то определитель матрицы равен нулю. Если матрица A невырожденная, её можно рассматривать как матрицу перехода от базиса
, а определитель матрицы, содержащий нулевой столбец равен нулю. Таким образом, если система векторов линейно зависима, то определитель матрицы равен нулю. Если матрица A невырожденная, её можно рассматривать как матрицу перехода от базиса  к
к 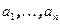 .
.
Система векторов  из арифметического пространства
из арифметического пространства  является линейной независимой тогда и только тогда, когда её можно дополнить до базиса всего пространства какими то векторами из системы
является линейной независимой тогда и только тогда, когда её можно дополнить до базиса всего пространства какими то векторами из системы  . По доказанной теореме, система
. По доказанной теореме, система  образует базис в том и только том случае, если определитель матрицы
образует базис в том и только том случае, если определитель матрицы  отличен от нуля. Определитель этой матрицы, с точность до знака, совпадает с минором k-го порядка матрицы
отличен от нуля. Определитель этой матрицы, с точность до знака, совпадает с минором k-го порядка матрицы  , получающегося вычёркиванием строчек с номерами
, получающегося вычёркиванием строчек с номерами  . Следовательно, система векторов
. Следовательно, система векторов  является линейно зависимой тогда и только тогда, когда все миноры k-го порядка матрицы
является линейно зависимой тогда и только тогда, когда все миноры k-го порядка матрицы  равны нулю. Оформим полученный результат в виде теоремы.
равны нулю. Оформим полученный результат в виде теоремы.
Теорема 7.9 Система  линейно зависима тогда и только тогда, когда все миноры k-го порядка матрицы
линейно зависима тогда и только тогда, когда все миноры k-го порядка матрицы  равны нулю.
равны нулю.