Линейные пространства.

Определение 7.1Множество V называется линейным пространством над числовым полем P, если определены две операции

1. сложения элементов из V (+)

2. умножения элемента из V на элемент из P (*)

Эти операции удовлетворяют аксиомам:

1. ассоциативность сложения, т.е. 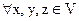(x+y)+z=x+(y+z)

2. коммутативность сложения, т.е. x+y=y+x

3. существование 0, т.е. x+0=x

4. существование обратного x+y=0, обратный обозначают –x.

5. ассоциативность умножения .

6. Дистрибутивность

7. Дистрибутивность

8. умножение на 0 0x=0. (в правой части 0 – элемент из V)

9. умножение на 1; 1x=x

Элементы линейного пространства называются векторами, а элементы числового поля P – скалярами.

Примеры линейных пространств.

1. Множество непрерывных функций над R

2. Множество векторов пространства над R

3. Арифметическое пространство (множество наборов из n чисел из P)

Определение 7.2Подмножество W линейного пространства V над полем P называется подпространством, если оно является пространством (в смысле выполняются все аксиомы)

Теорема 7.1. Для того, что бы подмножество W линейного пространства V над числовым полем P являлось подпространством необходимо и достаточно выполнения двух условий:

1.

2.

Примеры подпространств:

1. Множество многочленов образует подпространство в пространстве всех функций.

2. Множество решений системы линейных уравнений Ax=0 в арифметическом пространстве

3. Плоскость, прямая в пространстве векторов.

4. Линейная оболочка системы векторов (то есть множество всех линейных комбинаций векторов)

Следствие 7.1. Пересечение линейных подпространств является подпространством

Доказательство заключается в проверке выполнений условий Теорема 7.1.

Определение 7.3 Суммой подпространств V+W называется множество векторов вида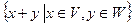

Следствие 7.2 Сумма подпространств – подпространство.

Доказательство заключается в проверке выполнений условий Теорема 7.1.

Следствие 7.3 Сумма подпространств V+W – наименьшее подпространство, которое содержит как V так и W.

Доказательство. Обозначим через F подпространство, являющееся пересечением всех подпространств содержащих подпространства V и W. Так как V+W содержит оба этих подпространства, то . Поскольку F содержит как V так и W, и является подпространством (Следствие 7.1), то сумма векторов x+y, где и 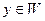, принадлежит F. Таким образом, установлено включение . Объединяя включения, получаем равенство V+W=F.