Введение

Конспект лекций

Моделирование систем и процессов

А.С. Морозов

Кафедра АИТП

 

 

 

 

 

Рязань 2014

Моделирование как создание некой системы — си­стемы-модели (второй системы), имеющей определенное сходство с системой-оригиналом (первой системой). Две эти реа­лизованные системы, из которых одна рассматривается как отобра­жение другой, связаны соотношениями подобия. Отображение одной системы в другой в этом случае является следствием выяв­ления сложных зависимостей между двумя системами, отраженных в соотношениях подобия.

Подобие явлений означает, что данные о протекании процессов, полученные при изучении одного явления, можно распространить на все явле­ния, подобные данным. При этом, однако, необходимо учитывать, что модель не дает и не должна давать подобия абсолютно всех процессов, содержащихся в явлении или так или иначе связанных с ним. Модель обеспечивает подобие только тех процессов, которые на ней исследуются.

Теория моделирования применяется:

а) при аналитическом отыскании зависимостей, соотношений и решений конкретных задач;

б) при обработке результатов экспериментальных исследований и испытаний различных технических устройств в тех случаях, когда результаты представлены в обобщенных «критериальных» зависи­мостях;

в) при создании моделей, воспроизводящих яв­ления в установках (оригиналах), обычно больших по величине или более сложных по структуре и более дорогих, чем модели (модели анализа);

г) при создании моделей установок, позволяющих синтезировать эффективные объекты.

Классифицируя моделирование по видам и группам, целесообразно прежде всего разделить их по признакам полноты и точности воспроизведения изучаемых процессов. Последнее осо­бенно важно, так как теория подобия и основанное на ней модели­рование не могут с абсолютной полнотой воспроизводить все сторо­ны и детали изучаемых явлений. Абсолютное подобие мо­жет мыслиться только отвлеченно и не может быть реализовано, так как это означало бы тождество, т. е. замену одного объекта или явления другим, точно таким же. Практические цели, преследуемые при решениях научных и технических задач, требуют применения моделирования в случаях, когда модель хорошо отражает изучае­мый объект (оригинал) только в отношении тех явлений или входящих в эти явления процессов, которые существенны в дан­ном исследовании, при данной постановке задачи. Таким образом, модель — это неполная копия объекта. Чтобы подчеркнуть это обстоятельство, иногда говорят, что «точная мо­дель не нужна, так как при точной модели нет подобия, а есть тождество», а слишком неточная бесполезна.

Модели, которые представ­ляют практический интерес, могут быть разделены на три (А, Б, В) способа (рис. В.2).

 

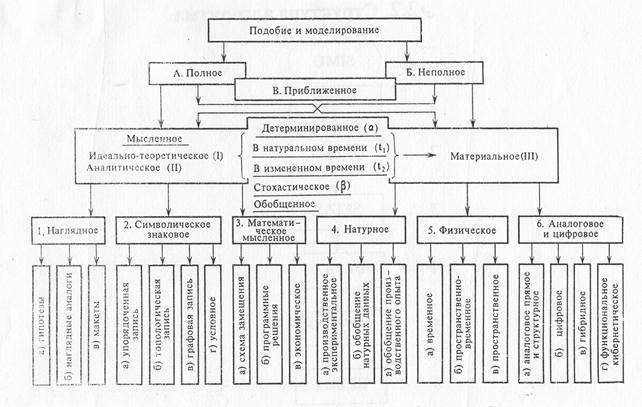
Рис. В.2. Основная классификация способов моделирования

ных соотношениях.

Из всего многообразия (рис. В.2) в дальнейшем рассмотрим только аналоговое (аналитическое), математическое и имитационное моделирование.

В инженерных задачах моделирование применяется в основном для проведения исследований на этапах проектирования, внедрения и эксплуатации сложных систем.

На этапах разработки технического и рабочего проектов систем моделирование служит для решения конкретных задач проектирования, обычно выбора оптимального по определенному критерию и при заданных ограничениях варианта системы из множества допустимых или для синтеза сложных систем.

Назначение моделирования на этапе внедрения и эксплуатации сложных систем – это проигрывание возможных ситуаций для принятия обоснованных и перспективных решений по управлению объектом. Моделирование (имитацию) также широко применяют при обучении и тренировке персонала автоматизированных систем управления, вычислительных комплексов и сетей, информационных систем в различных сферах. В этом случае моделирование носит характер деловых игр. Модель, реализуемая обычно на ЭВМ, воспроизводит поведение системы и внешней среды, а люди на основе полученных результатов в определенные моменты времени принимают решения по управлению системы.

Любую модель строят в зависимости от цели, которую ставит перед ней исследователь. Подобие процесса, протекающего в модели, реальному процессу является не целью, а условием правильного функционирования модели, и поэтому в качестве цели должна быть поставлена задача либо изучения какой-либо стороны функционирования объекта, либо определение его характеристик и т.п.

В свете изложенного, моделирование систем, как и любой производственной системы, предполагает определение состава и характеристик ее подсистем, элементов и связей между ними и внешней средой, описание процессов, протекающих в ней.

Элементы (подсистемы) можно описать тремя категориями: входы, процесс, выходы. Входы и выходы представляют собой финансовые, материальные или информационные потоки. Они имеют как непрерывный, так и дискретный характер. Процесс – это изменение состояние элементов во времени, которое может быть представлено вектором параметров, характеризующим процесс, он может меняться дискретно или непрерывно. Элементы могут иметь один и более как входов, так и выходов. Структура системы в свою очередь представляется взаимосвязанной совокупностью элементов (параметров).

Анализ и синтез технических решений систем опирается на математическое моделирование, которое позволяет решать следующие задачи:

· определение производительности всей системы и загрузки отдельных ее элементов;

· определение необходимых ресурсов производительности всех элементов системы;

· выделение наиболее существенных переменных, оценка степени влияния их изменения на исследуемые параметры системы, а также определение “узких мест”, т.е. технологических, организационных или управленческих факторов, наиболее существенно влияющих на показатели функционирования системы;

· изучение воздействий различных организационных, управленческих и технико-экономических изменений на показатели функционирования системы;

· оценка различных вариантов технических решений и стратегий управления при поиске оптимальной структуры систем.

Для моделирования систем используются как аналитическое, так и имитационное моделирование.

Аналитическое моделирование основано на косвенном описании моделируемого объекта с помощью аналитических формул. (алгебраических, интегродифференциальных, конечно-разностных, рядов и т.д.). Модель структурно не является подобной объекту моделирования и представляет формальную конструкцию, которую можно проанализировать и разрешить математическими средствами. Аналитические модели являются эффективным инструментом для решения задач оптимизации и вычисления в общем виде характеристик автоматизированных систем. Однако в ряде практических задач применение аналитических моделей затруднительно из-за их большой размерности и невозможности реализации средствами вычислительной техники. В таких случаях применяется имитационное моделирование, которое состоит в составлении вычислительного алгоритма и основано на прямом описании моделируемого объекта. При построении имитационной модели описываются законы функционирования каждого элемента объекта и связи между ними. Работа с имитационной моделью заключается в проведении имитационного эксперимента (сбор и обработка статистических данных), подобного процессу в реальном объекте. Поэтому исследования объекта на имитационной модели сводится к изучению на основе законов математической статистики характеристик процесса, протекающего в ходе эксперимента. Динамический процесс в модели протекает в так называемом системным времени, которое имитирует реальное время. Проведение имитационного моделирования часто оказывается трудоемкой и длительной процедурой и не может заменить аналитическое моделирование. Поэтому аналитическое и имитационное моделирование проводится в комплексе. Аналитическое моделирование используется для быстрого, но приближенного оценивания основных характеристик систем, а имитационное моделирование – для их уточнения.

Моделирование для исследования уже готовых объектов и процессов обычно проводится в виде организации эксперимента, обработки полученных экспериментальных данных, планирования эксперимента, позволяющего наглядно интерпретировать результаты (получить аналитическую зависимость описывающую, поведение системы при изменении параметров).

Моделирование для анализа и синтеза вновь создаваемых систем включает в себя:

1) определение параметров процессов и элементов на основе обследования и списания потоков, циркулирующих в объекте, его структуры, связей с внешней средой, а также постановки задачи и цели моделирования;

2) разработку концептуальной модели, включающую в себя разработку нескольких вариантов формализованных в общем виде и отвечающих поставленным задаче и цели моделей, выбор критерия оценки качества моделирования, выделения фрагмента объекта, подлежащего моделированию, выбор математического аппарата, описание переменных и декомпозиция модели;

3) разработку математической модели на основе выбранного математического аппарата (если выполняется имитационное моделирование, то ведется разработка моделирующего алгоритма);

4) выполнение программной реализации модели;

5) осуществление планирования проведения эксперимента и выбор средств обработки результатов эксперимента;

6) по результатам эксперимента составление заключения и выводов.

Задача курса «Моделирование систем и процессов» - дать студенту навыки по следующим вопросам:

1. Назначение, состав и основные задачи, решаемые с помощью математического моделирования.

2. Методики аналитического, имитационного моделирования, а также организации эксперимента и обработки экспериментальных данных.

3. Язык моделирования GPSS World.

Цель курса – на основе полученных знаний на практике выполнять следующее:

1. Разрабатывать аналитические и имитационные модели производственных систем.

2. По экспериментальным данным определять функциональные зависимости между параметрами систем и процессов.

3. Выполнять корреляционно-регрессивный анализ статистических данных, полученных в результате эксперимента.

4. Выполнять планирование модельных экспериментов.

5. Реализовывать модели на языке GPSS World.