Алгоритм разбиения средней точкой.

Последовательное осечение многоугольников. Алгоритм Сазермана - Ходтмена

 

 

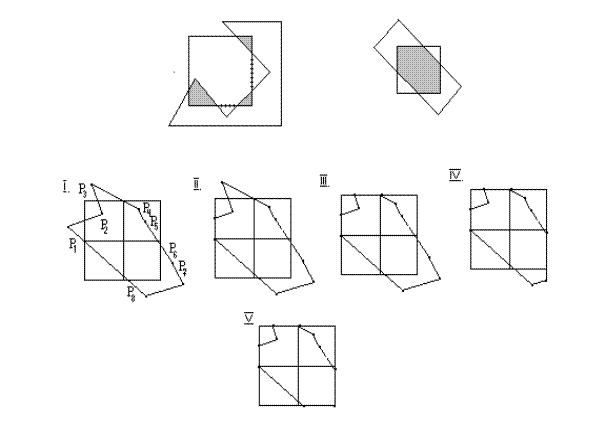Рассмотрим окно, имеющее экранные координаты левой, правой, нижней и верхней сторон: 0, 1023, 0, 1023 соотвественно. Экранные координаты концов отрезка с равны: Р₁(-307,631) и Р₂ (820,-136). Коды концевых точек равны: для Р₁ - (0001), а для Р₂ - (0100). Оба кода не равны нулю, поэтому отрезок не является полностью видимым. Логическое произведение кодов концевых точек равно (0000). Значит, отрезок нельзя тривиально отвергнуть как невидимый. Займемся поиском пересечений. Координаты средней точки с учетом округления равны:

xm =	x2 + x1 2	=	820 - 307 2	= 256.5 = 256
ym =	y2 + y1 2	=	-136 + 631 2	= 247.5 = 247

Код средней точки равен (0000). Оба отрезка Р₁Р_m и Р₂Р_m не являются ни полностью видимыми, ни тривиально невидимыми. Отложим на время отрезок Р₂Р_m и займемся отрезком Р₁Р_m. Процесс разбиения отрезков показан в табл. 3.1