Теоремы о пределах.

Пусть 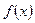и - функции, для которых существуют пределы при (или при ): , .

Сформулируем основные теоремы о пределах.

1. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, то есть

.

2. Предел произведения конечного числа функций равен произведению пределов этих функций, то есть

.

В частности, постоянный множитель можно выносить за знак предела, то есть .

3. Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), то есть

.

4. Если , то предел сложной функции f[(x)] равен

.

5. Теорема о переходе к пределу в неравенстве.

Если в некоторой окрестности точки

, то .

6. Теорема о пределе промежуточной функции.

Если в некоторой окрестности точки функция 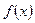заключена между двумя функциями и , имеющими одинаковый предел - число ,

то функция 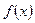имеет тот же предел ,

то есть, если

и ,

то

Первым замечательным пределомназывают,

Вторым замечательным пределомназывают

или

,

где число e = 2.71828… - иррациональное число, называемое неперовым числом, так как найдено Непером в XVII веке. Число e находит применение в математическом анализе, является основанием натуральных логарифмов.