Матрица парных корреляций. Мультиколлинеарность

Линейный корреляционный анализ позволяет установить прямые связи между переменными величинами по их абсолютным значениям. Формула расчета коэффициента корреляции построена таким образом, что если связь между признаками имеет линейный характер, коэффициент Пирсона точно устанавливает тесноту этой связи. Поэтому он называется также коэффициентом линейной корреляции Пирсона.

В общем виде формула для подсчета коэффициента корреляции такова:

 

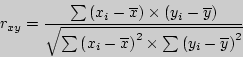
где 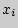- значения, принимаемые переменной X,

- значения, принимаемые переменой Y,

- средняя по X,

- средняя по Y.

Расчет коэффициента корреляции Пирсона предполагает, что переменные и распределены нормально.

Матрица парных коэффициентов корреляции представляет собой матрицу, элементами которой являются парные коэффициенты корреляции всех факторов модели.

Для нахождения в excel: КОРРЕЛ(массив1;массив2) Массив1 — это ячейка интервала значений.
Массив2 — это второй интервал ячеек со значениями.

Обращение к средствам анализа данных. Они доступны через команду Анализ данных меню Сервис.
Для вычисления матрицы коэффициентов парной корреляции R следует воспользоваться инструментом Корреляция.Инструмент Корреляцияприменяется, если имеется более двух переменных измерений для каждого объекта. В результате выдается таблица, корреляционная матрица, показывающая значение функции КОРРЕЛ для каждой возможной пары переменных измерений. Любое значение коэффициента корреляции должно находиться в диапазоне от -1 до +1 включительно.

По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности при использовании множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестаёт быть полностью независимой и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надёжна оценка распределения суммы объяснённой вариации по отдельным факторам с помощью МНК.

Если рассматривается регрессия y = a+b×x+c×z+d×v+e, то как одно из следствий системы нормальных уравнений получается равенство

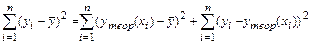. (5.11)

Общая сумма квадратов отклонений =

Сумма квадратов отклонений, объяснённая дисперсией (факторная) - SS регрессия

Остаточная сумма квадратов отклонений - SS остаток

Или

.

В свою очередь при независимости факторов друг от друга выполнимо равенство

,

где S_x, S_z, S_v – суммы квадратов отклонений, обусловленные влиянием соответствующих факторов.

Если факторы интеркоррелированы, последнее равенство нарушается.

Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:

затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в чистом виде, так как факторы коррелированы; параметры линейной регрессии теряют экономический смысл;

оценки параметров ненадёжны, обнаруживают большие стандартные ошибки и меняются с изменением объёма наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между векторами (МОПРЕД в EXCEL).

Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы г_xi,xj (x_i ¹ x_j) были бы равны нулю. Так, для включающего три объясняющих переменных уравнения

y_teor = b₀+b₁×x₁ + b₂×x₂ + b₃×x₃ + ε (5.12)

матрица коэффициентов корреляции между факторами имела бы определитель, равный 1

det(R)= .

Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции = 1, то определитель такой матрицы равен нулю:

Det(R) = .

Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадёжнее результаты множественной корреляции. Наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

Оценка значимости мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных H₀: det(R)=1. Доказано, что величина имеет приближённое c² –распределение с n×(n-1)/2 степенями свободы. Если фактическое значение c² превосходит табличное (критическое)

c²_факт > c² _{табл(df,a)},

то гипотеза Н₀ отклоняется. Это означает, что det(R) ¹ 1, недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной.

Через коэффициенты множественной детерминации можно найти переменные, ответственные за мультиколлинеарность факторов. Для этого в качестве зависимой переменной рассматривается каждый из факторов. Чем ближе значение коэффициента множественной детерминации к единице, тем сильнее проявляется мультиколлинеарность факторов. Сравнивая между собой коэффициенты множественной детерминации факторов

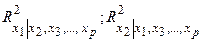и т.д.,

можно выделить переменные, ответственные за мультиколлинеарность, следовательно, можно решать проблему отбора факторов, оставляя в уравнении факторы с минимальной величиной коэффициента множественной корреляции.

Используя обозначение матрицы плана (для m = 3)

полная мультиколлинеарность означает следующие эквивалентные формулировки:

— столбцы матрицы X линейно зависимы между собой;

— ранг rank(X)<m+1;

— rank(X^T×X)<m+1;

— детерминант det(X^T×X) = 0.