Построение парной нелинейной регрессии. Оценка параметров. Вычисление коэффициента детерминации без процедур.

Cоотношение между социально-экономическими явлениями и процессами далеко не всегда можно выразить линейными функциями, так как при этом могут возникать неоправданно большие ошибки.

Так, например, нелинейными оказываются производственные функции (зависимости между объемом произведенной продукции и основными факторами производства – трудом, капиталом и т.п.), функции спроса (зависимость между спросом на товары или услуги и их ценами или доходом) и др.

Для оценки параметров нелинейных моделей используются два подхода.

Первый подход основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными.

Второй подход обычно применяется в случае, когда подобрать соответствующее линеаризующее преобразование не удается. В этом случае применяются методы нелинейной оптимизации на основе исходных переменных.

Для линеаризации модели в рамках первого подхода могут использоваться как модели, нелинейные по переменным, так и нелинейные по параметрам.

Если модель нелинейна по переменным, то введением новых переменных ее можно свести к линейной модели, для оценки параметров которой использовать обычный метод наименьших квадратов.

Так, например, если нам необходимо оценить параметры регрессионной модели

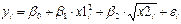, i=1, …, n,

то, вводя новые переменные Z1=x1², Z2 = , получим линейную модель

, i=1, …, n,

параметры которой находятся обычным методом наименьших квадратов.

Следует, однако, отметить и недостаток такой замены переменных, связанный с тем, что вектор оценок b получается не из условия минимизации суммы квадратов отклонений для исходных переменных, а из условия минимизации суммы квадратов отклонений для преобразованных переменных, что не одно и то же. В связи с этим необходимо определенное уточнение полученных оценок.

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. В известном учебнике по эконометрике [26] все нелинейные регрессии делятся на два класса:

1) регрессии, нелинейные по объясняющим переменным, но линейные по оцениваемым параметрам:

полиномы разных степеней

;

равносторонняя гипербола

;

2) регрессии, нелинейные по оцениваемым параметрам:

степенная ;

показательная ;

экспоненциальная .

Более сложной проблемой является нелинейность модели по параметрам, так как непосредственное применение метода наименьших квадратов для их оценивания невозможно. К числу таких моделей можно отнести, например, мультипликативную (степенную) модель.

Оценка параметров нелинейной регрессии по объясняющим переменным (первого класса) проводится также методом наименьших квадратов, так как эти функции линейны по параметрам.

Для любого полинома (многочлена) к-го порядка

с помощью замены переменных x₁ = x, x₁ = x², …, x_k = x^k получим линейную модель множественной регрессии

Следовательно, полином любого порядка сводится к линейной регрессии с её методами оценивания и проверки гипотез.

(ВНИМАНИЕ. ВТОРОЙ ПОДХОД МЫ БЛЯДЬ ДАЖЕ ПРИМЕРНО НЕ ИЗУЧАЛИ)

Рассмотрим теперь, как в MS EXCEL можно быстро построить модели парных нелинейных регрессий. Покажем это на данных примера 1.

Шаг 1. Сначала построим диаграмму (например, точечную или график) зависимости между Y и X.

Рис. 4.1. Построение диаграммы (точечной) зависимости между Y и X

Шаг 2. Устанавливаем точку мыши на одну из помеченных точек диаграммы, чтобы все точки зажглись жёлтым цветом. И тут же нажимаем на правую кнопку мыши. Возникнет окно диалога, в котором четвёртой строкой является фраза «Добавить линию тренда» (см. рис.4.2.). Левой кнопкой мыши выбираем эту четвёртую строку.

Рис. 4.2. Окно диалога при построении разных видов регрессии

Шаг 3. В появившемся окне диалога выберите тип зависимости между Y и X, например, логарифмический (см. рис. 4.3).

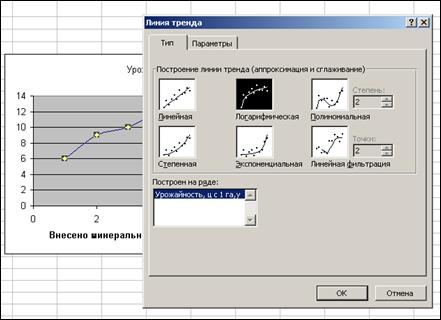
Рис. 4.3. Выбор нужной зависимости

Шаг 6. Выбираем закладку «Параметры» и устанавливаем левой кнопкой мыши флажки «Показывать уравнение на диаграмме», а также «Поместить на диаграмму величину достоверности аппроксимации (R^2)» (см. рис. 4.4).

Рис. 4.4. Установление флажков на закладке «Параметры»

Шаг 5. Нажмите «ОК». Получите диаграмму выбранной зависимости, изображённой на рисунке 4.5.

Рис. 4.5. Построение логарифмической зависимости между факторами Y и X

Замечание 1. Для аппроксимации исходных данных другой зависимостью между Y и X, начните с шага 1. Не забудьте после построения очередной зависимости перетащить полученную диаграмму на другое место, потому что MS EXCEL будет помещать диаграммы на одно и то же место на листе EXCELа.

Определение коэффициента детерминации:

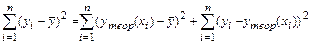. (5.11)

Общая сумма квадратов отклонений =

Сумма квадратов отклонений, объяснённая дисперсией (факторная) - SS регрессия

Остаточная сумма квадратов отклонений - SS остаток

R^2 = 1 - S^2ост/S^2общ = S^2факт/Sобщ

r_xy – выборочный коэффициент корреляции, определяемый следующим образом:

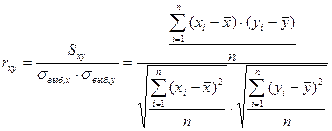(3.21)

и являющийся показателем тесноты связи между факторами x и y.

Здесь и – выборочные среднеквадратические отклонения случайных величин Х и Y, соответственно. Далее, эти величины будем обозначать как и . Таким образом, коэффициент регрессии пропорционален ковариации и коэффициенту корреляции, а коэффициенты пропорциональности служат для соизмерения перечисленных разномерных величин.

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции , называемый коэффициентом детерминации. Этот коэффициент характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:

. (3.22)

Соответственно, величина 1- характеризует долю дисперсии y, вызванную влиянием остальных, не учтённых в модели факторов.