Числовые характеристики непрерывных случайных величин. Нормальный закон и его параметры.
Материал основной части лекции.
ПЛАН
Владимир 2012
Л Е К Ц И Я
по дисциплине «Теория вероятностей и математическая статистика» для бакалавров направления 080100.62 «Экономика»
Тема № 2 . Случайные величины и их законы распределения .
Занятие № 2.8 Нормальный закон распределения случайных величин.
Вид занятия: лекция (11)
Литература: 1). Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб.пособие для вузов.-8-е изд.,стер.-М.:Высш.шк.,2002-479 с. (127-134). 2.) Вентцель Е.С. Теория вероятностей . Учебник М.: Гос.издат.физ.мат.лит-ры., 1958-464с.(108-102,114,115).
проведения занятия
| № п/п | Учебные вопросы занятия | Время, мин. | |
| I. II | Вводная часть: Объявление темы, темы занятия. Постановка учебных целей занятия. Основная часть. | 2-3 | |
| 1. Числовые характеристики непрерывных случайных величин .Нормальный закон и его параметры. 2. Вероятность попадания в заданный интервал нормальной случайной величины. Вычисление вероятности заданного отклонения. 3. Оценка отклонения теоретического распределения от нормального . Ассиметрия и эксцесс. | |||
| Заключительная часть | 2-3 | ||
| Подведение итогов занятия. Выдача задания на самостоятельную работу. | |||
Числовые характеристики непрерывных случайных величин
Распространимопределения числовых характеристик дискретных величин на непрерывные величины.
Начнем с математического ожидания.
Пусть непрерывная случайная величина Х задана плотностью распределения f(x). Допустим, что все возможные значения X принадлежат отрезку [а, b]. Разобьем этот
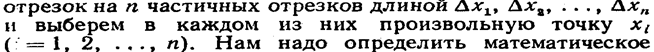
ожидание непрерывной' величины по аналогии с дискретной; составим сумму произведений возможных значений
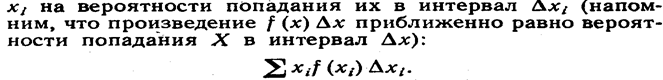
Перейдя к пределу при стремлении к нулю длины наибольшего из частичных отрезков, получим определенный
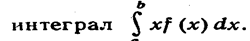
Математическим ожиданием непрерывной случайной величины- X, возможные значения которой принадлежат отрезку [а, b], называют определенный интеграл
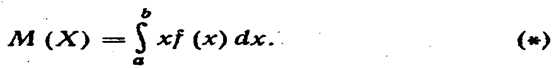 |
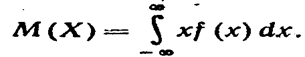 Если возможные значения принадлежат всей оси Ох, то
Если возможные значения принадлежат всей оси Ох, то
Предполагается, что несобственный интеграл сходится абсо-

это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) ниж-
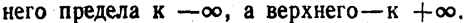
По аналогии с дисперсией дискретной величины определяется и дисперсия непрерывной величины.
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.
Если возможные значения Х принадлежат отрезку [а, b], то
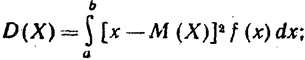 |