Модель Брауна (модель экспоненциального сглаживания).

Модель Брауна может отображать развитие не только в виде линейной тенденции, но также в виде случайного процесса, не имеющего тенденции, а также в виде изменяющейся па­раболической тенденции. Соответственно различают модели Брауна:

• нулевого порядка, которая описывает процессы, не имею­щие тенденции развития. Она имеет один параметр (оценка текущего уровня). Прогноз развития на k шагов вперед осуществляется согласно формуле . Такая модель также называется «наивной» («будет, как
было»);

• первого порядка . Коэффициент значение, близкое к последнему уровню, и представляет как бы закономерную составляющую этого уровня. Коэф­фициент 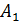определяет прирост, сформировавшийся в ос­новном к концу периода наблюдений, но отражающий также (правда, в меньшей степени) скорость роста на более ранних этапах;

• второго порядка, отражающей развитие в виде парабо­лической тенденции с изменяющимися «скоростью» и «ускорением». Она имеет три параметра 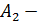оценка текущего прироста или «ускорение»). Прогноз осуществ­ляется по формуле: .
Порядок модели обычно определяют либо априорно на основе визуального анализа графика процесса (есть ли тренд и близок ли он к линейной функции), знаний законов раз­вития характера изменения исследуемого явления, либо методом проб, сравнивая статистические характеристики моделей различного порядка на участке ретроспективного прогнозирования.

Рассмотрим этапы построения линейной адаптивной модели Брауна.

Этап 1. По первым пяти точкам временного ряда оце­ниваются начальные значения и 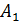параметров модели с помощью метода наименьших квадратов для линейной ап­проксимации:

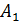Этап 2. С использованием параметров и по модели Брауна находим прогноз на один шаг (k = 1):

Этап 3. Расчетное значение экономического пока­зателя сравнивают с фактическим и вычисляется вели­чина их расхождения (ошибки). При k = 1 имеем:

.

Этап 4. В соответствии с этой величиной корректируются параметры модели. В модели Брауна модификация осущест­вляется следующим образом:

;

,

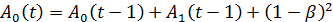где 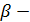коэффициент дисконтирования данных, изменяю­щийся в пределах от 0 до 1 ( ), характеризующий обесценение данных за единицу времени и отражающий степень доверия более поздним наблюдениям. Оптимальное значение находится итеративным путем, т. е. многократ­ным построением модели при разных и выбором наилуч­шей, или по формуле:

,

где 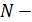длина временного рада, параметр сглаживания ;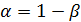

ошибка прогнозирования уровня Y(t), вычис­ленная в момент времени (t - 1) на один шаг вперед.

Этап 5. По модели со скорректированными параметрами и 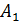находят прогноз на следующий момент времени. Возврат на пункт 3, если .

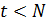Если ,то построенную модель можно использовать для прогнозирования на будущее.

Этап 6. Интервальный прогноз строится как для линей­ной модели кривой роста.

Пример 3.Построим прогноз по линейной модели Брауна курса немецкой марки за май 1997 г.

Исходный временной ряд содержит 19 уровней наблю­дения данного показателя:

 

Воспользуемся схемой адаптивного прогнозирования. Начальные оценки параметров получим по первым пяти точкам (табл. 5.6) при помощи МНК по формулам:

,

,

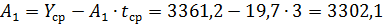где среднее значение фактора «время»; 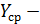среднее значение исследуемого показателя .

Таблица 5.6. Оценка начальных значений параметров модели

№п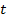
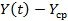
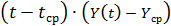
			4,0 1,0 0,0 1,0 4,0	-28,2 -24,2 -7,2 2,8 56,8	-2 -1	56,4 24,2 2,8 113,6
			10,0	0,0

 

Возьмем k = 1, а параметр сглаживания равным 0,4. В табл. 5.7 приведены расчеты параметров модели Брауна на каждом шаге. На последнем шаге получена модель . Прогнозные оценки по этой модели получаются подстановкой в нее значений k = 1 и k = 2, а интервальные — по формуле:

 

,

 

где, как и в формуле (5.18), среднее квадратическое отклонение (СКО) аппроксимации, табличное значение критерия Стьюдента с заданным уровнем значимости .

На рис. 5.1 представлены результаты аппроксимации и прогнозирования по этой модели. Ряд 1 соответствует фак­тическим данным, ряд 2 — расчетным данным по модели Брауна, при этом указаны точечные прогнозы на два шага вперед. Интервальные прогнозы можно получить, используя приведенные в табл. 5.7 значения 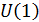и .

Таблица 5.7. Оценка параметров модели Брауна

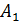
		3302,1 3331,2 3339,5 3354,7 3365,4 3412,3 3398,9 3385,5 3404,4 3397,5 3408,5 3411,2 3424,0 3412,8 3415,4 3416,6 3404,9 3390,0 3390,5 3389,8	19,7 21,5 19,0 18,3 16,8 22,5 15,7 10,2 11,8 8,3 8,8 7,6 8,6 4,8 4,4 3,8 0,9 -2,2 -1,7 -1,5	3321,8 3352,7 3358,5 3373,0 3382,3 3434,8 3414,5 3395,7 3416,2 3405,8 3417,3 3418,8 3432,6 3417,6 3419,8 3420,4 3405,8 3387,9 3388,8	11,2 -15,7 -4,5 -9,0 35,7 -42,8 -34,5 10,3 -22,2 3,2 -7,3 6,2 -23.6 -2,6 -3,8 -18,4 -18,8 3,1 1,2
				3388,3 3386,9

 

Прогнозирование курса немецкой марки по модели Брауна

 

№№№№№№№№№№№№№№№№№№№№№№№№№№№№№№№№№№№№№№

№№№№№№№№№№№№№№№№№№№№№№№№№№№№№№№№№№№

Рис. 5.1. Результаты аппроксимации и прогнозирования по адаптивной модели Брауна (параметр сглаживания равен 0,4)

В моделях Брауна и Хольта параметры сглаживания харак­теризуют степень адаптации модели к изменению ряда наблю­дений Они определяют скорость реакции модели на измене­ния, происходящие в развитии. Чем они больше, тем быст­рее реагирует модель на изменения. Обычно для устойчивых рядов их величина большая, а для неустойчивых — маленькая. В различных методах прогнозирования используется раз­личный подход к их определению. Их можно взять фиксиро­ванными, а наилучшее значение определить методом подбора, чтобы ошибка прогноза на один шаг вперед была наименьшей. При использовании компьютера это не представляет труда.

Альтернативу этому подходу составляет динамическое изменение параметров сглаживания. В методах эволюции и симплекс-планирования параметры адаптации постоянно меняются на каждом шаге. Для каждого параметра сглажи­вания формируется несколько значений.

Модели и методы авторегрессии. В авторегрессионных (АР) моделях текущее значение процесса представляется как линейная комбинация предыдущих его значений и слу­чайной компоненты.

Идентификация АР(р) модели состоит в определении ее порядка р. Одной из предпосылок построения модели этого типа является применение их к стационарному процессу. Поэтому в более широком смысле идентификация модели включает также выбор способа трансформации исходного ряда наблюдений, как правило, имеющего некоторую тен­денцию, в стационарный (или близкий к нему) ряд. Один из наиболее распространенных способов решения этой про­блемы — последовательное взятие разностей, т.е. переход от исходного ряда к ряду первых, а затем и вторых разностей.

return false">ссылка скрыта

«Чистые» авторегрессионные процессы имеют плавно за­тухающую автокорреляционную функцию (АКФ). В этом случае в качестве порядка модели выбирается лаг, после ко­торого все частные автокорреляционные функции (ЧАКФ) имеют незначительную величину. Однако на практике ред­ко встречаются процессы, которые легко было бы идентифи­цировать. Поэтому порядок модели обычно определяется ме­тодом проб из нескольких альтернатив. В число кандидатов включаются модели, у которых порядок соответствует ЧАКФ, превышающей стандартное отклонение 1/N. При обработке разностных рядов иногда ориентируются на АКФ, выбирая модели, у которых порядок соответствует максимальному ее значению, при условии, что оно превышает стандартное от­клонение.

Ряды без тенденции, как правило, не представляют инте­реса для экономистов. АР-модели вообще не предназначены для описания процессов с тенденцией, однако они хорошо описывают колебания, что весьма важно для отображения развития неустойчивых показателей.

Чтобы сделать возможным применение АР-моделей к процессам с тенденцией, на первом этапе формируют ста­ционарный ряд, т. е. исключают тенденцию путем перехода от исходного временного ряда к ряду Z(t) (t = 1, 2, ..., N-d) первых или вторых разностей (d = 1 или 2).

 

Например, ряд первый разностей формируется как ряд приростов, т. е. последовательным вычитанием двух соседних уровней. С учетом этого АР(р) — модель порядка р имеет вид:

Параметры этой модели вычисляются по МНК с учетом сложности модели либо методом адаптивной фильтрации (МАФ). В обоих случаях необходимо предварительно иден­тифицировать модель, т. е. правильно определить порядок разностного ряда d и порядок модели р.

Простейшим способом определения наиболее подходящего разностного ряда является вычисление для каждого ряда (d = 0,1,2) его дисперсии, т. е. усредненной суммы квадратов расхождений его уровней со средним значением .Для дальнейшей обработки выбирается ряд, у которого величина этого показателя минимальна.

Для идентификации порядка модели обычно используется автокорреляционная функция, значения которой определя­ются по формуле:

где количество уровней стационарного ряда ( );

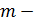номер коэффициента автокорреляции ( ).

В качестве порядка модели принимается номер коэффи­циента автокорреляции r(m), имеющего максимальную ве­личину. Следовательно, в модели используются р уровней, которые оказывают на текущий уровень наибольшее влияние. В соответствии с МНК формируется система из р уравнений, которая в компактной форме имеет вид:

.

Например, для р = 2 система принимает вид:

В ней суммирование проводится по в пределах от 3 до n = N-d.

Решив эту систему уравнений, получают числовое значе­ние .Оценка свободного члена получается из со­отношения:

.

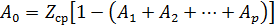На основе построенной модели вычисляют прогнозное значение разностного ряда Z(n+k) на k шагов вперед, а от него переходят к прогнозной оценке исходного ряда.

Так, для d = 1 имеем:

 

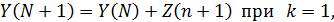
Следовательно, прогнозные оценки базируются как на фактических, так и на полученных прогнозных уровнях ряда. Доверительный интервал прогноза рассчитывается на основе точечного прогноза:

верхняя граница прогноза ,

нижняя граница прогноза .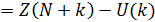

Величина U(k) рассчитывается по формуле:

,

где среднеквадратичесая ошибка вычисленная с учетом сложности

модели; коэффициент, соответствующий табличному значению статистики Стьюдента с выбранным уровнем зна­чимости ; коэффициент под квадратным корнем рассчиты­вается рекуррентно, причем при j = 0 величина С(0) = 1, а при; j>0

.

В методе адаптивной фильтрации используется АР(р)-модель без свободного члена. Ее параметры корректируются на й ите­рации в каждый момент времени следующим образом:

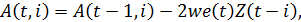
где и векторы новых и старых значений параметров (весов) модели;

w — константа обучения, определяющая скорость адаптации параметров модели (w>0);

e(t) — ошибка прогнозирования уровня Y(t).

Алгоритм построения модели прогнозирования состоит в следующем. На первой итерации (J = 1) на основе начально­го набора весов и первых р уровней ряда вычисляется и его расхождение с фактическим уровнем, т.е. 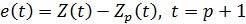. Подставляя величину ошибки в уравнение кор­ректировки весов, получают новый набор весов для следую­щего момента времени 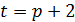. Далее эта процедура повто­ряется для следующих 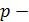наборов ,каждый из которых образован из предыдущего исключением первого и добавлением одного нового уровня ряда. Если на итерации / оптимальные веса не получены, то на следующей итерации надо вернуться к первому набору уровней ряда но уже с новыми началь­ными весами, взятыми от предыдущей итерации.

Определение начальных весов осуществляется путем ре­шения уравнения Юла—Уокера, составленного на основе ко­эффициентов автокорреляции. Процедура корректировки параметров заканчивается, когда среднеквадратическая ошибка перестает существенно убывать или при достижении заданного максимального количества итераций.

Пример 4.Рассмотрим построение прогноза на основе мо­делей авторегрессии. Ниже в табл. 5.8 и 5.9 приведены рас­четы построения прогноза курса немецкой марки, выпол­ненные с использованием программы ОЛИМП; при этом в качестве лучшей модели из всего класса адаптивных моде­лей, реализованных в программе, выбрана авторегрессион­ная модель. На рис. 5.2 представлены результаты аппрокси­мации и прогнозирования по этой модели.

Таблица 5.8. Модель временного ряда «Немецкая марка»