Прогнозирование экономической динамики на основе трендовых моделей

Прогнозирование экономических показателей на основе трендовых моделей, как и большинство других методов эко­номического прогнозирования, основано на идее экстраполя­ции. Как уже сказано выше, под экстраполяцией обычно понимают распространение закономерностей, связей и соот­ношений, действующих в изучаемом периоде, за его пределы. В более широком смысле слова ее рассматривают как полу­чение представлений о будущем на основе информации, от­носящейся к прошлому и настоящему. В процессе построения прогнозных моделей в их структуру иногда закладываются элементы будущего предполагаемого состояния объекта или явления, но в целом эти модели отражают закономерности, наблюдаемые в прошлом и настоящем, поэтому достоверный прогноз возможен лишь относительно таких объектов и яв­лений, которые в значительной степени детерминируются прошлым и настоящим.

Существуют две основные формы детерминации: внут­ренняя и внешняя. Внутренняя детерминация, или самодетер­минация, более устойчива, ее проще идентифицировать с ис­пользованием экономико-математических моделей. Внешняя детерминация определяется большим числом факторов, по­этому учесть их все практически невозможно. Если некоторые методы моделирования, например адаптивные, отражают об­щее совокупное влияние на экономическую систему внеш­них факторов, т.е. отражают внешнюю детерминацию, то ме­тоды, базирующиеся на использовании трендовых моделей экономических процессов, представленных одномерными временными рядами, отражают внутреннюю детерминацию объектов и явлений.

При экстраполяционном прогнозировании экономической динамики на основе временных рядов с использованием трен­довых моделей выполняются следующие основные этапы:

1) предварительный анализ данных;

2) формирование набора моделей (например, набора кри­вых роста), называемых функциями-кандидатами;

3) численное оценивание параметров моделей;

4) определение адекватности моделей;

5) оценка точности адекватных моделей;

6) выбор лучшей модели;

7) получение точечного и интервального прогнозов;

8) верификация прогноза.

Порядок реализации первых шести этапов из перечислен­ных описан в предыдущих параграфах данной главы. Рассмот­рим более подробно два заключительных этапа.

Прогноз на основании трендовых моделей (кривых роста) содержит два элемента: точечный и интервальный прогнозы. Точечный прогноз — это прогноз, которым называется единст­венное значение прогнозируемого показателя. Это значение оп­ределяется подстановкой в уравнение выбранной кривой рос­та величины времени t, соответствующей периоду упреждения: и т. д. Такой прогноз называется точеч­ным, так как на графике его можно изобразить в виде точки.

Очевидно, что точное совпадение фактических данных в будущем и прогностических точечных оценок маловероятно. Поэтому точечный прогноз должен сопровождаться двусто­ронними границами, т.е. указанием интервала значений, в котором с достаточной долей уверенности можно ожидать появления прогнозируемой величины. Установление такого интервала называется интервальным прогнозом.

Интервальный прогноз на базе трендовых моделей осу­ществляется путем расчета доверительного интервала — такого интервала, в котором с определенной вероятностью можно ожидать появления фактического значения прогнози­руемого экономического показателя. Расчет доверительных интервалов при прогнозировании с использованием кривых роста опирается на выводы и формулы теории регрессий. Перенесение выводов теории регрессий на временные эконо­мические ряды не совсем правомерно, так как динамиче­ские ряды, как выше уже отмечали, отличаются от стати­стических совокупностей. Поэтому к оцениванию довери­тельных интервалов для кривых роста следует подходить с известной долей осторожности.

Методы, разработанные для статистических совокупно­стей, позволяют определить доверительный интервал, зави­сящий от стандартной ошибки оценки прогнозируемого показателя, от времени упреждения прогноза, от количества уровней во временном ряду и от уровня значимости (ошибки) прогноза.

Стандартная (среднеквадратическая) ошибка оценки прогнозируемого показателя определяется по формуле:

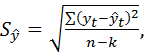(5.17)

где фактическое значение уровня временного ряда для времени ; расчетная оценка соответствующего показа­теля по модели (например, по уравнению кривой роста); количество уровней в исходном ряду; число парамет­ров модели.

В случае прямолинейного тренда для расчета доверительно­го интервала можно использовать аналогичную формулу для парной регрессии, таким образом доверительный интервал прогноза Uу в этом случае будет иметь вид

, (5.18)

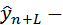где период упреждения; точечный прогноз по модели на 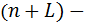ймомент времени; количество наблю­дений во временном ряду; стандартная ошибка оценки прогнозируемого показателя, рассчитанная по ранее приве­денной формуле для числа параметров модели, равного двум; t_a — табличное значение критерия Стьюдента для уровня значимости и для числа степеней свободы, равного .

В выражение (5.18) введем обозначение

.

С учетом этого формула для доверительного интерва­ла примет вид

. (5.19)

Значения величины К для оценки доверительных интер­валов прогноза относительно линейного тренда табулированы. Фрагмент такой таблицы для уровня значимости а = 0,20 пред­ставлен для иллюстрации в табл. 5.4.

Таблица 5.4

Число уровней в ряду (n)	Период упреждения L
	1,932 1,692 1,581 1,536	2,106 1,774 1,629 1,572	2,300 1,865 1,682 1,611	2,510 1,964 1,738 1,658	2,733 2,069 1,799 1,697	2,965 2,180 1,863 1,745

 

Иногда для расчета доверительных интервалов прогноза относительно линейного тренда применяют приведенную выше формулу в несколько преобразованном виде:

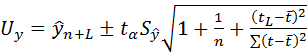, (5.20)

 

где порядковый номер уровня ряда ; время, для которого делается прогноз; время, соответствующее середине периода наблюдений для исходного ряда, например,

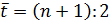; суммирование ведется по всем наблюдениям.

Эту формулу можно упростить, если, как часто делается на практике, перенести начало отсчета времени на середину периода наблюдений (F= 0):

 

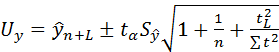, (5.21)

 

Формула для расчета доверительных интервалов прогноза относительно тренда, имеющего вид полинома второго или третьего порядка, выглядит следующим образом:

. (5.22)

 

Аналогично вычисляются доверительные интервалы для экспоненциальной кривой роста, а также для кривых роста, имеющих асимптоту (модифицированная экспонента, кривая Гомперца, логистическая кривая), если значение асимптоты известно.

Таким образом, формулы расчета доверительного интер­вала для трендовых моделей разного класса различны, но каждая из них отражает динамический аспект прогнозиро­вания, т.е. увеличение неопределенности прогнозируемого процесса с ростом периода упреждения проявляется в посто­янном расширении доверительного интервала.

Несмотря на громоздкость некоторых формул, расчет точеч­ных и интервальных прогнозов на основе трендовых моделей в форме кривых роста технически является достаточно простой процедурой. Однако не следует обольщаться технической простотой процедуры экстраполяции и пытаться заглянуть слишком далеко, это неизбежно приведет к грубым ошибкам. Оптимальная длина периода упреждения определяется отдель­но для каждого экономического явления с учетом статисти­ческой колеблемости изучаемых данных на основе содержа­тельного суждения о стабильности явления. Эта длина, как правило, не превышает для рядов годовых наблюдений одной трети объема данных, а для квартальных и месячных рядов — двух лет.

При выравнивании временных рядов с использованием кривых роста приходится решать вопрос о том, какой длины должен быть ряд, выбираемый для прогнозирования. Оче­видно, что если период ряда экономической динамики слиш­ком короткий, можно не обнаружить тенденцию его развития. С другой стороны, очень длительный временной ряд может охватывать периоды с различными трендами и его описание с помощью одной кривой роста не даст положительных ре­зультатов. Поэтому рекомендуется поступать следующим образом. Если нет никаких соображений качественного по­рядка, следует брать возможно больший промежуток времени.

Если развитие обнаруживает циклический характер, следует брать период от середины первого до середины последнего периода цикла. Если ряд охватывает периоды с разными трендами, лучше сократить ряд, отбросив наиболее ранние уровни, которые относятся к периоду с иной тенденцией развития.

При экстраполяционном прогнозировании экономической динамики с использованием трендовых моделей весьма ва­жным является заключительный этап — верификация прогноза.Верификация любых дескриптивных моделей, к которым относятся трендовые модели, сводится к сопостав­лению расчетных результатов по модели с соответствующи­ми данными действительности — массовыми фактами и за­кономерностями экономического развития. Верификация прогнозной модели представляет собой совокупность крите­риев, способов и процедур, позволяющих на основе многосто­роннего анализа оценивать качество получаемого прогноза. Однако чаще всего на этапе верификации в большей степени осуществляется оценка метода прогнозирования, с помощью которого был получен результат, чем оценка качества самого результата. Это связано с тем, что до сих пор не найдено эф­фективного подхода к оценке качества прогноза до его реа­лизации.

Даже в тех случаях, когда прогноз не оправдался, нельзя категорически утверждать, что он был бесполезен, поскольку пользователь, если он хотя бы частично контролирует ход событий и может воздействовать на экономический процесс, может использовать прогнозную информацию желаемым для себя образом. Так, получив прогноз событий, определяю­щих нежелательное направление перспективного развития, пользователь может принять меры, чтобы прогноз не оп­равдался; такой прогноз называется само деструктивным. Если прогноз предсказал ход событий, устраивающий поль­зователя, то он может использовать свои возможности для увеличения вероятности правильного прогноза; подобный прогноз называется саморегулирующим. Таким образом, по­казателем ценности прогноза является не только его дос­товерность, но и полезность для пользователей.

О точности прогноза принято судить по величине ошиб­ки прогноза — разности между фактическим значением ис­следуемого показателя и его прогнозным значением. Оче­видно, что определить указанную разность можно лишь в двух случаях: либо если период упреждения уже окончился и известно фактическое значение прогнозируемого показате­ля (известна его реализация), либо если прогнозирование осуществлялось для некоторого момента времени в про­шлом, для которого известны фактические данные.

Во втором из названных случаев информация делится на две части. Часть, охватывающая более ранние данные, слу­жит для оценивания параметров прогностической кривой роста, другая, более поздняя, рассматривается как реализа­ция прогноза. Полученные таким образом ошибки прогноза в какой-то мере характеризуют точность применяемой мето­дики прогнозирования.

Проверка точности одного прогноза недостаточна для оценки качества прогнозирования, так как она может быть результатом случайного совпадения. Наиболее простой мерой качества прогнозов при условии, что имеются данные об их реализации, является отношение числа случаев, когда фак­тическая реализация охватывалась интервальным прогнозом, к общему числу прогнозов. Данную меру качества прогнозов k можно вычислить по формуле

где 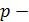число прогнозов, подтвержденных фактическими данными; число прогнозов, не подтвержденных факти­ческими данными.

Однако в практической работе проблему качества про­гнозов чаще приходится решать, когда период упреждения еще не закончился и фактическое значение прогнозируемого показателя неизвестно. В этом случае более точной счита­ется модель, дающая более узкие доверительные интервалы прогноза. На практике не всегда удается сразу построить достаточно хорошую модель прогнозирования, поэтому опи­санные в данной главе этапы построения трендовых моде­лей экономической динамики выполняются неоднократно.

Рассмотрим пример расчета точечного и интервального прогноза на основе трендовых моделей, используя данные задачи, решаемой в предыдущем параграфе данной главы.

Пример 2. Пусть для временного ряда, представлен­ного в табл. 5.3, требуется дать прогноз на два шага вперед ( ) на основе адекватной линейной модели .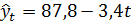

Точечные прогнозы получим, подставляя в уравнение модели значения :

.

.

При расчете доверительных интервалов прогноза учтем, что в процессе решения упомянутой задачи предыдущего параграфа было найдено значение средней квадратической ошибки оценки прогнозируемого показателя , а значения величины К в формуле (5.17) для ряда из девяти уровней можно получить при уровне значимости из табл. 5.4 путем линейной интерполяции приведенных значений для п = 7 и п = 10: для t = 10 (L = 1) К = 1,77; для t = 11 (L = 2) К = 1,88. Результаты расчета по формуле (5.17) представлены в табл. 5.5.

Таблица 5.5

Время	Шаг	Точечный прогноз	Доверительный интервал прогноза
Нижняя граница	Верхняя граница
		53,8 50,4	51,3 47,8	56,3 53,0

 

Так как модель, на основе которой осуществлялся про­гноз, признана адекватной, то с принятым уровнем значи­мости 0,20, другими словами, с доверительной вероятностью 0,80 (или 80%) можно утверждать, что при сохранении сло­жившихся закономерностей развития прогнозируемая вели­чина попадет в интервал, образованный нижней и верхней
границами.