Демонстративный пример

Пример1. Для временного ряда, представленного графе 2 табл. 5.3, рассчитать параметры полинома первой степени (линейная модель). Оценить адекватность и точность построенной модели и с вероятностью 0.95 произвести прогноз уровня на 2014 год.

Таблица 5.3

Годы
Уровни

Для того, чтобы определить параметры полинома первой степени необходимо построит систему нормальных уравнении:

.

 

Вычисление коэффициентов этой системы и модельных значении уровней сведем в таблицу 5.4.

 

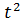
Годы Фактические уровни     Модельные уровни  
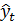
84,4 81,0 77,6 74,1 70,7 67,3 63,8 60,4 57,0  
Итого 636,3  

 

На основании таблицы 5.4 составим систему нормальных уравнении:

.

Решим эту систему и получим:

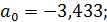
На основании полученных данных составим модель тренда:

.

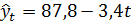Подставляя в модель тренда текущие номера уровней, получим модельные значения. Они приведены в таблице 5.4.

Перейдем теперь к оценке адекватности и точности построенной модели.

Проверку случайности уровней ряда остатков проведем на основе критерии пиков (поворотных точек). Прежде всего, сформируем остаточную последовательность (ряд остатков), для чего из фактических значений уровней ря­да вычтем соответствующие расчетные значения по модели. Эти и другие необходимые вычисления для проверки случайности уровней ряда остатков сведены в таблице 5.5.

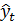
Фактические уровни   Модельные уровни Остатки Точки пиков или
84,4 81,0 77,6 74,1 70,7 67,3 63,8 60,4 57,0 0,6 0,0 0,4 -2,1 -1,7 2,7 0,2 0,6 -1,0 - -
Итого 636,3 -0,3

 

Следовательно, количество пиков Для проверки случайности остатков найдем математическое ожидание и дисперсию для пиковых точек по формулам:

Далее проверим выполнение неравенства:

Найдем правую часть неравенства:

Следовательно

Таким образом, с доверительной вероятностью можно сделать вывод, что свойство случайности ряда остат­ков подтверждается.

Результаты предыдущей проверки дают возможность про­вести проверку соответствия остаточной последовательности нормальному закону распределения. Для проверки этой гипотезы и с целью дальнейших расчетов введем дополнительную таблице 5.6.

 

 
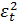
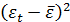
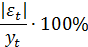
0,6 0,0 0,4 -2,1 -1,7 2,7 0,2 0,6 -1,0 0,36 0,00 0,16 4,41 2,89 7,29 0,04 0,36 1,00 0,63 0,03 0,43 -2,07 -1,67 3,00 0,23 0,63 -0,97 0,40 0,00 0,18 4,28 2,79 9,00 0,05 0,40 0,94 - -0,6 0,4 -2,5 0,4 4,4 -2,5 0,4 -1,6 - 0,36 0,16 6,25 0,16 19,36 6,25 0,16 2,56 0,71 0,00 0,51 2,92 2,46 3,86 0,31 0,98 1,79
Итого -0,3 16,51 0,01 18,04 - 35,62 13,54

 

Проверку гипотезы о соответствия остаточной последовательности нормальному закону распределения воспользуемся RS-критерием. Определим размах вариации и среднее квадратическое отклонение. Для этого воспользуемся формулами:

 

;

Следовательно, критерий:

 

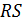По таблицам по числу уровней и уровня значимости найдем нижний и верхний границы интервала. И они равны соответственно и . Так как значение попадает в интервале между нижней и верхней границами табличных значений данного критерия, это по­зволяет сделать вывод, что свойство нормальности распреде­ления выполняется.

 

Чтобы проверить равенства (близости) нулю матема­тического ожидания ряда остатков, необходимо вычислить стандартное (среднеквадратическое) отклонение для этой последовательности и расчетное значение критерия Стьюдента. Определим их значения по формулам:

Для числа степеней свободы и уровня значимости по таблицам найдем табличное значение критерии Стьюдента и она равна Поскольку расчетное значение меньше табличного значения, поэтому гипотеза о равенстве нулю математического ожидания случайной последовательности принимается.

Для проверки независимости уровней ряда остатков (отсут­ствия автокорреляции) вычислим значение критерия Дарбина—Уотсона по формуле:

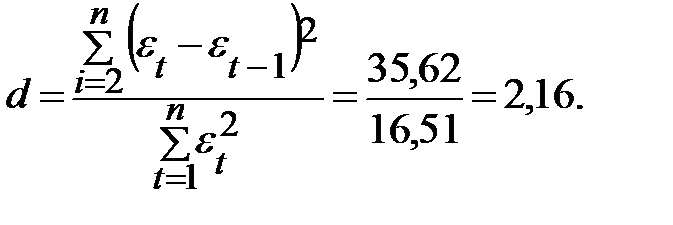
Для числа степеней свободы , уровня значимости и количество параметров по таблицам найдем табличные значения нижней и верхней границ интервала. И они равны соответственно и 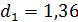. Так как расчетное значение критерия d больше верхнего табличного значения ,то гипотеза о независимости уров­ней остаточной последовательности, т.е. об отсутствии в ней автокорреляции, принимается.

Из сказанного выше следует, что остаточная последова­тельность удовлетворяет всем свойствам случайной компо­ненты временного рада, следовательно, построенная линейная модель является адекватной.

Для характеристики точности модели воспользуемся по­казателем средней относительной ошибки аппроксимации, который рассчитывается по формуле:

 

Полученное значение средней относительной ошибки говорит о достаточно высоком уровне точности по­строенной модели (ошибка менее 5% свидетельствует об удовлетворительном уровне точности; ошибка в 10 и более процентов считается очень большой).