Тема: «Параметры процедур и функций».
Варианты индивидуальных заданий:
В каждом варианте задания одну или несколько функций передавать в качестве параметров других подпрограмм, используя с этой целью процедурный тип. При выполнении заданий значения исходных данных выберите самостоятельно.
Вариант 1.
Составить подпрограмму вычисления длины дуги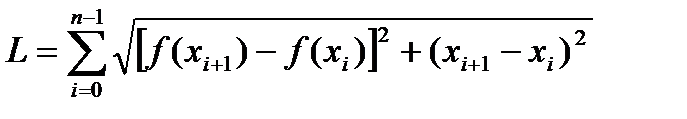 
, образованной функцией f(x) в интервале [а, b]. Используя подпрограмму, определить самую длинную из дуг, образованных функциями f1(x)=х2+ 2ln(1+x2), f2(x)=x ln x2 -2x, f3(x)=(x2 +2x-3)e-x на интервале [a, b].
Вариант 2.
Составить подпрограмму определения минимума функции y=f(x), заданной в дискретных точках отрезка [а, b] спостоянным шагом h. Используя ее, найти минимумы функций y1=sin2х cos x –ln[x], у2=х2-2х+8.
Вариант 3.
Составить подпрограмму определения максимума функции у=f(x), заданной в дискретных точках отрезка [а, b] с постоянным шагом h. Используя ее, найти максимумы функций: y1=e-xcos2x-1; у2=х ln[x+1].
Вариант 4.
Составить подпрограмму определения минимума функции z=f(x,y), заданной в дискретных точках xi=x0+ihx, уj,=у0+jhy (i=1…nx, j=1…nv ). Используя ее, найти минимумы функций z1=3x2-2у2+4ху-8х, z2=6x2+y2-4x-6y+1.
Вариант 5.
Составить подпрограмму определения максимума функции z=f(x, у), заданной в дискретных точках хi=х0+ihx , yj=у0 +jhy (i=1…nx , j=1…ny ). Используя ее, найти максимумы функций z1=6x2+у2 — 2ху+2, z2=2x2+3y2+2х+3у-3ху.
Вариант 6.
Составить подпрограмму вычисления определенного интеграла по формуле прямоугольников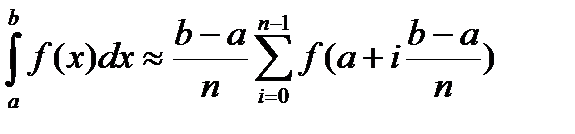 
и, используя ее, вычислить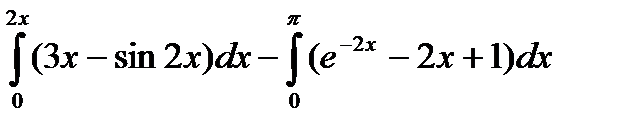 
Вариант 7.
Составить подпрограмму вычисления площади треугольника, заданного координатами своих вершин, по формуле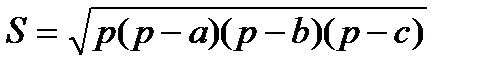 
, где р=(а+b+с)/2; а, b, с — длины сторон треугольника. Вычислять с использованием подпрограммы-функции как расстояние между вершинами треугольника (по формуле, приведенной в варианте 1). Найти суммарную площадь двух заданных треугольников.
Вариант 8.
Составить подпрограмму вычисления коэффициента корреляции двух случайных величин x: и у на основании выборок x=(х1, х2, ..., хn), у=(у1, y2,…, уn) по формуле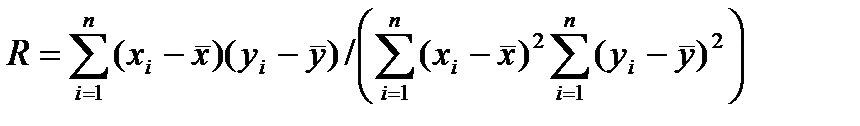 
. Для вычисления 
, 
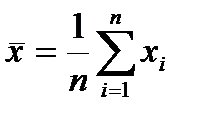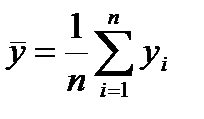использовать подпрограмму-функцию. Найти R для произвольных выборок двух случайных величин х, у.
Вариант 9.
Составить подпрограмму вычисления высот треугольника со сторонами а, b, с по формулам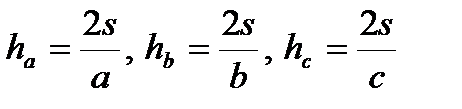 
, где 
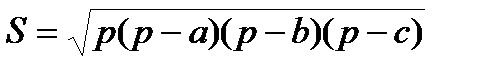, p=(a+b+c)/2, если заданы координаты вершин треугольника. Для определения длин сторон а, b, с использовать подпрограмму-функцию вычисления длины отрезка между двумя точками (по формуле, приведенной в варианте 1). Найти наименьшую из высот заданного треугольника.
Вариант 10.
Cоставить подпрограмму определения координат точки пересечения двух прямых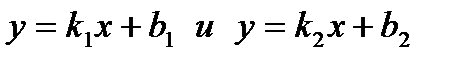 
проходящих через заданные тонки, по формулам 
. Коэффициенты k и b прямой у=kx+b, проходящей через точки (x1,y1), (x2,y2), вычислить исходя из уравнения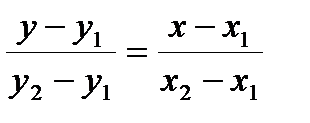 
с использованием подпрограммы-функции. Найти точку пересечения двух заданных прямых.
Вариант 11.
Составить подпрограмму вычисления компонент вектора градиента функции F(х1, х2 ,... , хn) п переменных в точке Х=(х1, х2,..., хn) по конечно-разностным формулам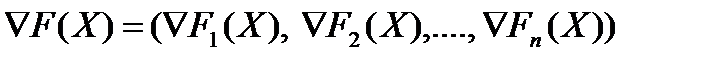 
, где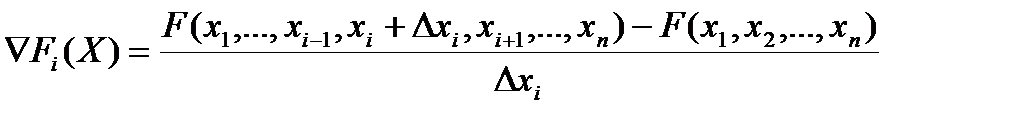 
Найти вектор градиента для функций z1=2x2 — 4у2+ 8ху — 2х+1, z2=8x2 — 2ху взаданной точке (х, у) при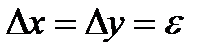 
.
Вариант 12.
Составить подпрограмму вычисления k-йстепени квадратной матрицы из п*п элементов, используя подпрограмму умножения двух матриц. Найти А3, В2, где А, В — произвольные квадратные матрицы.
Вариант 13.
Составить подпрограмму упорядочения элементов одномерного массива по убыванию их значений методом выбора максимального элемента, используя подпрограмму нахождения номера максимального элемента в последовательности чисел. Упорядочить по убыванию массивы Х и Y.
Вариант 14.
Составить функцию определения косинуса угла между двумя векторами по формул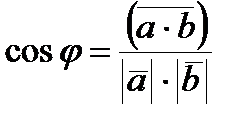е 
, где 
. Для вычисления скалярного произведения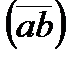 
и модуля 
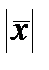использовать функции. Найти косинусы углов между заданными векторами.
Вариант 15.
Составить подпрограмму определения номера строки матрицы с максимальной характеристикой. Для вычисления характеристики использовать подпрограмму-функцию. В качестве характеристики строки рассмотреть следующие величины:
а) сумму положительных элементов;
б) среднее арифметическое всех элементов.
Найти строки с соответствующими максимальными характеристиками для произвольных матриц X и Y.
Вариант 16.
Составить подпрограмму определения минимальной характеристики в прямоугольной матрице. Для вычисления характеристики использовать подпрограмму. В качестве характеристики рассмотрены следующие величины:
а) произведение элементов каждого столбца матрицы;
б) максимальный элемент столбца матрицы.
Найти соответствующие минимальные характеристики для заданных матриц А и В.
Вариант 17.
Составить подпрограмму определения номеров строк матрицы с минимальной и максимальной характеристиками. Для вычисления характеристики использовать подпрограмму-функцию. В качестве характеристики рассмотреть следующие величины:
а) среднее арифметическое элементов каждой строки матрицы;
б) число положительных элементов в строке.
Поменять местами строки с максимальной и минимальной характеристиками типа а) в заданной матрице А и б) в заданной матрице В.
Вариант 18.
Составить подпрограмму табулирования произвольной функции: вычисления множества значений z={zi}, i=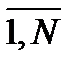 
, функции z=f(x) для заданного множества значений аргумента x={xi}, i= 
. Используя ее, найти множества zl, z2 значений двух функций
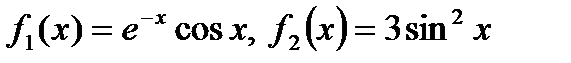для двух заданных множеств значений аргумента х: Х1={xi}, i= 
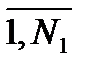; Х2={хi}, i=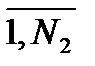 
Вариант 19.
Назовем характеристикой строки двумерного символьного массива число элементов, относящихся к гласным русским буквам. Составить подпрограмму замены символов в строке с максимальной характеристикой на символ '*'. Произвести указанную замену символов в произвольном исходном массиве. Характеристику определить с помощью функции.
Вариант 20.
Составить подпрограмму, которая присваивает элементам одномерного массива Z значения функции f(x) в точках (х1, х2, ..., хn). Сформировать одномерные массивы из значений функций f1=e-хcosx, f2=3sin2х в заданных точках.
Вариант 21.
Найти полную поверхность треугольной пирамиды, заданной координатами своих вершин, используя подпрограмму-функцию вычисления длины отрезка между двумя точками (по формуле, приведенной в варианте 1).
Вариант 22.
Найти объем правильной треугольной пирамиды, заданной длиной своего ребра.
Вариант 23.
Даны координаты вершин треугольника и координаты точки внутри его. Найти расстояние от данной точки до ближайшей стороны треугольника.
Вариант 24.
Вычислить с точностью до ε интеграл 
по формуле прямоугольников (см. вариант 6).
Вариант 25.
Составить подпрограмму определения максимума функции z=f(x, у), заданной в дискретных точках хi=х0+ihx , yj=у0 +jhy (i=1…nx , j=1…ny ). Используя ее, найти максимумы функций z1=3x2+у2 — 3ху+4, z2=3x2+y2+5х +3у — 8ху.