Оценка адекватности и точности трендовых моделей

Независимо от вида и способа построения экономико-ма­тематической модели вопрос о возможности ее применения в целях анализа и прогнозирования экономического явле­ния может быть решен только после установления адекват­ности, т.е. соответствия модели исследуемому процессу или объекту. Так как полного соответствия модели реальному процессу или объекту быть не может, адекватность — в ка­кой-то мере условное понятие. При моделировании имеется в виду адекватность не вообще, а по тем свойствам модели, которые считаются существенными для исследования.

Трендовая модель 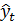конкретного временного ряда счи­тается адекватной, если остаточная компонента удовлетворяет следующим свойствам:

• случайностью колебаний уровней остаточной последова­тельности;

• соответствием распределения случайной компоненты нормальному закону распределения;

• равенством математического ожидания случайной ком­поненты нулю;

• независимостью значений уровней случайной последо­вательности, то есть отсутствием существенной авто­корреляции.

Рассмотрим, каким образом осуществляется проверка этих свойств остаточной последо­вательности.

Проверка случайности колебаний уровней остаточной последовательностиозначает проверку гипотезы о правиль­ности выбора вида тренда. Для исследования случайности отклонений от тренда мы располагаем набором разностей:

Характер этих отклонений изучается с помощью ряда непараметрических критериев. Одним из таких критериев является критерий серий, основанный на медиане выборки. Ряд из величин располагают в порядке возрастания их значений и находят медиану полученного вариационного ряда, т.е. срединное значение при нечетном n или среднюю арифметическую из двух срединных значений при n четном. Возвращаясь к исходной последовательности и сравни­вая значения этой последовательности с , будем ставить знак «плюс», если значение превосходит медиану, и знак «минус», если оно меньше медианы; в случае равенства сравниваемых величин соответствующее значение опус­кается. Таким образом, получается последовательность, состоящая из плюсов и минусов, общее число которых не превосходит n. Последовательность подряд идущих плюсов или минусов называется серией. Для того чтобы последова­тельность была случайной выборкой, протяженность самой длинной серии не должна быть слишком большой, а общее число серий — слишком малым.

Обозначим протяженность самой длинной серии через , а общее число серий —через . Выборка признается случайной, если выполняются следующие неравенства для 5%-ного уровня значимости:

 

 

где квадратные скобки, как обычно, означают целую часть числа.

Если хотя бы одно из этих неравенств нарушается, то ги­потеза о случайном характере отклонений уровней времен­ного ряда от тренда отвергается и, следовательно, трендовая модель признается неадекватной.

Другим критерием для данной проверки может служить критерий пиков (поворотных точек, максимумов). Уровень последова­тельности считается максимумом, если он больше двух рядом стоящих уровней, т.е. , и минимумом, если он меньше обоих соседних уровней, т.е. . В обоих случаях считается поворотной точкой. Общее чис­ло поворотных точек для остаточной последовательности обозначим через .

В случайной выборке математическое ожидание числа точек поворота и дисперсия выражаются формулами:

 

 

Критерием случайности с 5% -ным уровнем значимости, т.е. с доверительной вероятностью 95%, является выполнение неравенства:

(5.9)

 

где квадратные скобки, как и ранее, означают целую часть числа.

Если это неравенство нарушается, то ги­потеза о случайном характере отклонений уровней времен­ного ряда от тренда отвергается и, следовательно, трендовая модель признается неадекватной.

Проверка соответствия распределения случайной ком­поненты нормальному закону распределенияможет быть произведена лишь приближенно с помощью исследования показателей асимметрии 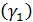и эксцесса ( 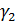),так как временные ряды, как правило, не очень велики. При нормальном рас­пределении показатели асимметрии и эксцесса некоторой генеральной совокупности равны нулю. Мы предполагаем, что отклонения от тренда представляют собой выборку из генераль­ной совокупности, поэтому можно определить только выбороч­ные характеристики асимметрии и эксцесса и их ошибки:

 

 

 

 

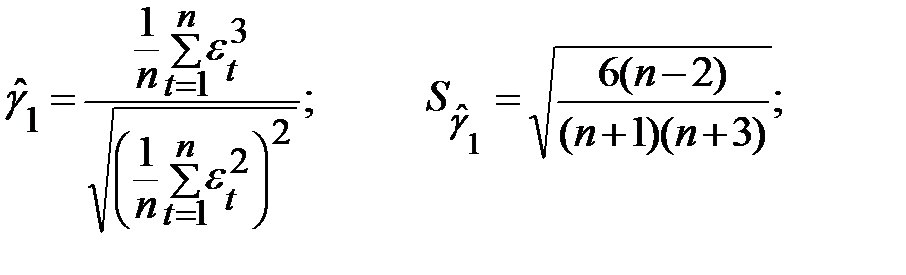
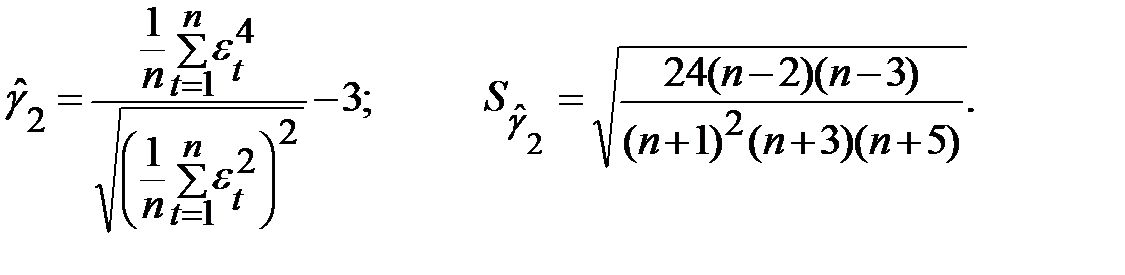
В этих формулах выборочная характеристика асим­метрии; выборочная характеристика эксцесса; и соответствующие среднеквадратические ошибки.

Если одновременно выполняются следующие неравенства:

 

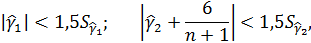
то гипотеза о нормальном характере распределения случайной компоненты принимается.

Если выполняется хотя бы одно из неравенств:

 

то гипотеза о нормальном характере распределения отверга­ется, трендовая модель признается неадекватной. Другие случаи требуют дополнительной проверки с помощью более сложных критериев.

Кроме рассмотренного метода известен ряд других методов проверки нормальности закона распределения случайной величины: метод Вестергарда, RS-критерий и т. д. Рассмот­рим наиболее простой из них, основанный на RS-критерии. Этот критерий численно равен отношению размаха вариа­ции случайной величины R к стандартному отклонению S.

В нашем случае , а .

Вы­численное значение RS-критерия сравнивается с табличными (критическими) нижней и верхней границами данного отношения, и если это значение не попадает в интервал между критическими границами, то с заданным уровнем значимости гипотеза о нормальности распределения отвергается; в про­тивном случае эта гипотеза принимается. Для иллюстрации приведем несколько пар значений критических границ RS-критерия для уровня значимости : при ниж­няя граница равна 2,67, а верхняя равна 3,685; при эти числа составляют соответственно 3,18 и 4,49; при они равны 3,47 и 4,89.

Проверка равенства математического ожидания слу­чайной компоненты нулю,если она распределена по нор­мальному закону, осуществляется на основе критерия Стьюдента. Расчетное значение этого критерия задается формулой

, ()

где среднее арифметическое значение уровней остаточ­ной последовательности ;

стандартное (среднеквадратическое) отклонение для этой последовательности и рассчитывается по формуле:

Если расчетное значение t меньше табличного значения статистики Стьюдента с заданным уровнем значимости а и числом степеней свободы 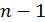, то гипотеза о равенстве нулю математического ожидания случайной последовательности принимается; в противном случае эта гипотеза отвергается и модель считается неадекватной.

Проверка независимости значений уровней случайной компоненты,т.е. проверка отсутствия существенной авто­корреляции в остаточной последовательности может осуще­ствляться по ряду критериев, наиболее распространенным из которых является d-критерий Дарбина—Уотсона. Рас­четное значение этого критерия определяется по формуле

()

Заметим, что расчетное значение критерия Дарбина-Уотсона в интервале от 2 до 4 свидетельствует об отрицательной связи; в этом случае его надо преобразовать по формуле ив дальнейшем использовать значение .

Расчетное значение критерия d (или d') сравнивается с верхним и нижним критическими значениями ста­тистики Дарбина—Уотсона, фрагмент табличных значений которых для различного числа уровней ряда п и числа опре­деляемых параметров модели k представлен для наглядности в табл. 5.2 (уровень значимости 5%).

 

1,08 1,20 1,35 1,36 1,41 1,49 0,95 1,10 1,28 1,54 1,54 1,57 0,82 1,00 1,21 1,75 1,68 1,65

 

Если расчетное значение критерия d больше верхнего табличного значения ,то гипотеза о независимости уров­ней остаточной последовательности, т.е. об отсутствии в ней автокорреляции, принимается. Если значение d меньше нижнего табличного значения ,то эта гипотеза отвергается и модель неадекватна. Если значение d находится между значениями и ,включая сами эти значения, то считается, что нет достаточных оснований сделать тот или иной вывод и необходимы дальнейшие исследования, например, по боль­шему числу наблюдений.

Вывод об адекватности трендовой модели делается, если все указанные выше четыре проверки свойств остаточной последовательности дают положительный результат.

Для адекватных моделей имеет смысл ставить задачу оценки их точности. Точность модели характеризуется величиной отклонения модельных значении уровней от фактических значении.

В качестве стати­стических показателей точности применяются следующие:

среднеквадратическое отклонение

 

, (5.13)

средняя относительная ошибка аппроксимации

 

, (5.14)

коэффициент сходимости

 

, (5.15)

коэффициент детерминации

и другие показатели; в приведенных формулах количе­ство уровней ряда, число определяемых параметров модели, оценка уровней ряда по модели, среднее арифметическое значение уровней ряда.

На основании указанных показателей можно сделать выбор из нескольких адекватных трендовых моделей эконо­мической динамики наиболее точной, хотя может встре­титься случай, когда по некоторому показателю более точна одна модель, а по другому — другая.

Данные показатели точности моделей рассчитываются на основе всех уровней временного ряда и поэтому отражают лишь точность аппроксимации. Для оценки прогнозных свойств модели целесообразно использовать так называемый ретроспективный прогноз — подход, основанный на выде­лении участка из ряда последних уровней исходного вре­менного ряда в количестве, допустим, уровней в качестве проверочного, а саму трендовую модель в этом случае следует строить по первым точкам, количество которых будет равно . Тогда для расчета показателей точности модели по ретроспективному прогнозу применяются те же формулы, но суммирование в них будет вестись не по всем наблюде­ниям, а лишь по последним газ наблюдениям. Например, формула для среднего квадратического отклонения будет иметь вид:

 

,

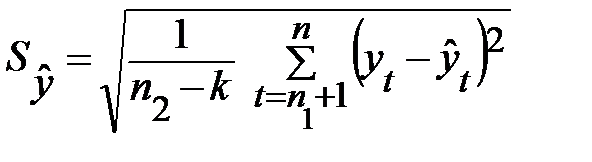где значения уровней ряда по модели, построенной для первых уровней.

Оценивание прогнозных свойств модели на ретроспектив­ном участке весьма полезно, особенно при сопоставлении различных моделей прогнозирования из числа адекватных. Однако надо помнить, что оценки ретро прогноза — лишь приближенная мера точности прогноза и модели в целом, так как прогноз на период упреждения делается по модели, построенной по всем уровням ряда.