Тренд-сезонные экономические процессы и их анализ

Рассмотрим ряд проблем и основных понятий, связанных с исследованием сезонных колебаний в экономике. Сезон­ность, как правило, связывается исключительно со сменой природно-климатических условий в рамках ограниченного промежутка времени — годового периода. Наиболее ярко эта связь видна там, где исследуемые процессы прямо связаны с естественными особенностями того или иного времени года. Например, в сельском хозяйстве, добывающих отраслях, отраслях легкой промышленности, обрабатывающих сельскохозяйственную продукцию, и др. Однако сезонные колебания формируются не только под влиянием природно-климатических факторов, но и, пусть в меньшей мере, под влиянием иных особенностей системы, уходящих корнями в экономику.

Влияние сезонности на экономику вполне очевидно и проявляется в аритмии производственных и других процессов: недогрузка производственных мощностей в одни периоды года и более интенсивное их использование в другие; нерав­номерное распределение внутри рамок года объемов грузооборота и товарооборота и т.д. Не во всех случаях сезон­ность является следствием действия неуправляемых или почти неуправляемых факторов. Чаще всего они поддаются регулированию. Но даже и в тех случаях, когда прямое воз­действие на процессы, вызывающие сезонные колебания, не­возможно, необходимо учитывать их действие при совершен­ствовании технологических, организационно-экономических процессов и процессов управления. Для того чтобы можно было целенаправленно влиять на сезонность, необходимо уметь измерять и анализировать сезонность, уметь предвидеть развитие процессов, подверженных сезонным колебаниям.

Под сезонными колебаниями понимают регулярные, пе­риодические наступления внутригодовых подъемов и спадов производства, грузооборота и товарооборота и т. д., связан­ных со сменой времени года, а под сезонностью — ограни­ченность годового периода работ под влиянием того же при­родного фактора.

Как отмечено выше, упорядоченная во времени последо­вательность наблюдений экономического процесса называ­ется временным рядом, и если процесс подвержен периоди­ческим колебаниям, имеющим определенный и постоян­ный период, равный годовому промежутку, то мы имеем дело с так называемым тренд-сезонным временным рядом (сезонным временным рядом).

Почти всюду, где не оговорено специально, будем рас­сматривать тренд-сезонный временной ряд , ,по­рождаемый аддитивным случайным процессом:

 

, (5.27)

где тренд;

сезонная компонента;

случайная компонента;

число уровней наблюдения.

Относительно предполагается, что это некоторая гладкая функция, степень гладкости которой заранее неизвестна. Сезон­ная компонента имеет период : ( 12 для ря­да месячных данных; для ряда квартальных данных).

Кроме того, известно, что нацело делит , т.е. , 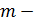целое число. Очевидно, если число месяцев или кварталов в году, то 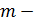число лет, представленных во вре­менном ряду . Часто исходные данные тренд-сезонного временного ряда представляются в виде матрицы , раз­мера [ ]. В этом случае выражение (5.27) перепишется с учетом введения двойной индексации:

, (5.28)

 

 

Запишем соотношения, устанавливающие связь между индексами t и :

 

(5.29)

 

Постараемся выделить и кратко охарактеризовать зада­чи, возникающие при исследовании сезонности вообще и се­зонных временных рядов в частности. Проблема анализа се­зонности заключается в исследовании собственно сезонных колебаний и в изучении того внешнего циклического меха­низма, который их вызывает. Для исследования сезонных колебаний вне связи с причинами, их порождающими, оче­видно, необходимо отфильтровать из временного ряда сезонную компоненту и затем уже анализировать ее ди­намику. Большинство методов фильтрации построено таким образом, что предварительно выделяется тренд, а затем уже сезонная компонента. Тренд в чистом виде необходим и для анализа динамики сезонной волны.

При исследовании сезонной волны чаще всего пред­полагается, что она не изменяется год от года, т.е. , На самом же деле такое предположение далеко от действительности, по крайней мере, для большинства эконо­мических процессов. Для сезонной волны характерно изме­нение со временем, как ее размаха, так и формы. В резуль­тате возникает необходимость в анализе и предсказании изменений сезонной волны.

Перечислим теперь задачи, которые возникают при исследовании сезонных временных рядов:

1) определение наличия во временном ряду тренда и
определение степени его гладкости;

2) выявление наличия во временном ряду сезонных
колебаний;

3) фильтрация компонент ряда;

4) анализ динамики сезонной волны;

5) исследование факторов, определяющих сезонные коле­бания;

6) прогнозирование тренд-сезонных процессов.
Объясним суть некоторых понятий и дадим краткую

характеристику каждого пункта. Под степенью гладкости тренда мы будем понимать минимальную степень полинома, адекватно сглаживающего компоненту .Этот пункт ис­пользуется в некоторых итерационных алгоритмах фильтра­ции при выделении из временного ряда его компонент , , .

Выявление наличия во временном ряду сезонных коле­баний сводится к проверке на случайность остаточного ряда:

.

Под фильтрацией компонент ряда понимается выделение из ряда его составляющих , , .

Анализ динамики, или эволюции, сезонной волны может рассматриваться как процесс решения трех взаимосвязан­ных задач:

1. Анализ динамики амплитуды сезонной волны в каж­дом месяце (квартале, неделе).

2. Анализ динамики точек экстремума сезонной волны.

3. Исследование изменений формы волны.

Выше уже отмечалось, что в каких бы формах ни прояв­лялась сезонность, в любом случае ее действие отрицательно сказывается на результатах деятельности предприятия, фирмы, отрасли, экономики в целом. Управление сезонностью долж­но опираться на знание законов ее эволюции, на знание внеш­ней среды, в которой происходит развитие процесса, подвер­женного сезонным колебаниям.

Будем иллюстрировать отдельные вопросы анализа се­зонности в экономических процессах на конкретных данных. В табл. 4.6 приведен временной ряд ежемесячных объемов перевозок грузов морским транспортом в условных едини­цах. На рис. 4.2 представлены ежемесячные объемы перево­зок за 1-й, 4-й, 7-й, 10-й и 13-й годы, т.е. с дискретностью три года. Визуально нетрудно заметить, что исследуемому ряду присущ возрастающий тренд и повторяющиеся из года в год подъемы и спады объемов перевозок в одни и те же пе­риоды года, т. е. сезонные колебания. Таким образом, про­цесс, характеризуемый этим временным рядом, относится к тренд-сезонным экономическим процессам. Для данного ряда , т = 13, так что =156.

Таблица 5.6. Объемы перевозок грузов морским транспортом в условных единицах

Год	Месяц
	7,62 8,50 9,40 8,84 9,15 10,80 11,86 10,84 12,19 13,21 14,08 14,73 14,29	6,80 8,11 9,00 10,18 8,02 10,24 11,47 11,55 12,48 12,46 13,19 13,66 14,32	9,02 9,93 11,44 11,64 10,87 12,63 12,81 13,31 14,84 15,33 15,26 17,59 17,50	9,67 10,70 11,73 12,49 12,01 13,50 14,34 14,78 15,65 16,40 16,30 17,74 18,10	10,70 11,24 13,05 13,38 13,96 15,03 15,54 16,08 16,84 17,44 17,78 19,97 19,82	11,48 11,98 13,09 13,63 14,39 15,33 16,61 16,60 17,32 17,26 18,07 19,28 19,71	11,43 12,38 13,74 13,88 14,41 15,24 15,22 16,41 17,69 17,89 18,31 19,44 19,94	11,68 12,73 13,74 13,82 14,45 15,02 15,83 16,72 17,62 17,76 18,71 19,95 20,94	11,20 11,84 12,41 13,11 13,56 14,51 15,46 16,65 16,39 16,97 18,25 19,58 19,96	10,77 12,19 13,69 12,96 13,39 14,12 14,83 15,68 16,37 16,85 17,70 18,23 19,31	9,34 10,97 10,68 12,01 12,40 13,09 13,93 14,67 15,19 15,78 15,87 17,41 18,52	6,55 10,63 10,45 10,75 12,05 12,35 14,00 14,75 14,17 14,86 16,47 16,87 17,85

 

Статистические методы определения наличия тренда рас­смотрены в § 4.2. Например, применение метода Фостера— Стьюарта для временного ряда, представленного в табл. 4.6, дает следующие значения статистик Стьюдента для ряда в среднем и дисперсии:

.

При уровне значимости , т. е. с доверительной вероятностью 0,95, и при числе степеней свободы табличное значение критерия Стьюдента равно . Так как и ,то гипотезы об отсутствии тенденции, как в среднем текущем значении ряда, так и в диспер­сии отвергаются, т. е. в данном временном ряду присутст­вуют тренд и тенденции в дисперсии ряда.

Рассмотрим, прежде всего, некоторые теоретические во­просы выявления и фильтрации сезонной компоненты вре­менного экономического ряда. По-прежнему будем рассмат­ривать временные ряды, порождаемые аддитивным случай­ным процессом (4.19). Определим понятия сглаживания и фильтрации. Под сглаживанием тренд-сезонного временного ряда будем понимать процесс получения оценок , а под фильтрацией компонент — процесс получения оценок , и . В настоящее время развиваются три основных направления фильтрации компонент временного ряда вида (4.19): регрессионные, спектральные и итерационные. Ниже мы рассмотрим более подробно итерационные методы фильтрации.

Итерационные методы фильтрации.При выделении (фильтрации) компонент временного ряда с помощью тех или иных методов неизбежно встает вопрос о «чистоте» фильтрации, т.е. вопрос о степени близости оценок и их истинным значениям , .Следует отметить, что пока ни один из известных методов не обеспечивает необходимой степени чистоты фильтрации для временных рядов различ­ной структуры.

Итерационные методы фильтрации составляющих вре­менного ряда появились в свое время как результат признания невозможности выделения компонент ряда прямыми мето­дами. Основная идея итерационных процедур заключается в многократном применении скользящей средней:

 

(5.30)

 

и одновременной оценке сезонной компоненты в каждом цикле. При этом переход от одного шага итерационной процедуры к другому может сопровождаться изменением параметров скользящей средней. Если формулу для сколь­зящей средней записать в виде

 

(5.31)

то при переходе от одной итерации к другой может проис­ходить изменение длины участка скольжения Т' и закона изменения весовых коэффициентов . В некоторых итера­ционных методах, кроме того, используется регрессия (как правило, линейная) исходного ряда на преобразованный в первом шаге ряд .

Итерационные методы отличает простота и удовлетвори­тельная «чистота» фильтрации компонент ряда. Однако всем им присущ и весьма существенный недостаток. При­менение скользящей средней (5.30) и (5.31) приводит к потере части информации на концах временного ряда. Напри­мер, если используется скользящая средняя вида (5.30), то на каждом конце ряда теряется по его членов.

Далее рассмотрим два итерационных метода: Четверикова и Шискина—Эйзенпресса [9].

Метод Четверикова. 1. Эмпирический ряд выравни­вается скользящей средней (4.22) с периодом скольжения , т.е. берется ( ) членов исходного ряда, из которых первый и последний берутся с половинным весом: . Выпадающие членов ряда с обоих его концов либо восстанавливаются экстраполированием выравненного ряда, либо остаются в стороне при последующей стадии работ.

Получаются предварительная оценка тренда

и отклонения эмпирического ряда от выравненного

или

(5.32)

 

2. Для каждого года i вычисляется среднеквадратическое отклонение, на которое и делятся затем отдельные месячные (квартальные) отклонения соответствующего года:

 

(5.33)

где

 

. (5.34)

 

3. Из «нормированных» таким путем отклонений вы­числяется предварительная средняя сезонная волна:

 

. (5.35)

 

4. Средняя предварительная сезонная волна умножается на среднеквадратическое отклонение каждого года и вычи­тается из эмпирического ряда:

. (4.36)

5. Получающийся таким образом ряд, лишенный пред­варительной сезонной волны, вновь сглаживается скользящей средней (для месячных данных по пяти или семи точкам в зависимости от интенсивности мелких конъюнктурных коле­баний и продолжительности более крупных). В результате получается новая оценка тренда .

6. Отклонения эмпирического ряда от ряда ,полу­ченного в п.5

, (4.37)

вновь подвергаются аналогичной обработке по пп. 2 и 3 для выявления окончательной средней сезонной волны.

7. Исключение окончательной сезонной волны произво­дится после умножения средней сезонной волны на коэффициент напряженности сезонной волны:

(4.38)

где выравненные значения ряда, случайная компонента:

.

Описанный метод был разработан Четвериковым в 1928г. и в отличие от разработанных ранее методов простой средней, метода Персонса и других позволял исключать влияние сезон­ных волн переменной структуры.

Метод Шискина—Эйзенпресса.В методике Шискина— Эйзенпресса, кроме скользящей средней (5.30), на втором и последующих этапах итерационной процедуры применяются более сложные пятнадцати- и двадцатиодноточечные скользя­щие Спенсера. Они имеют соответственно следующий вид:

 

или в цифровой записи Кенделла:

В (4.32) и (4.33) символы [N]означают выравнивание ряда скользящей средней. Так, например, если N = 5, то

Символ означает двойное последовательное выравнива­ние ряда одной и той же скользящей средней, т.е. если N = 5, то сначала получаем выравненные оценки по (4.34), затем к ним применяем ту же скользящую среднюю (4.34):

Если рассматривается двадцатиодноточечная скользящая средняя (4.31), то затем мы должны были бы применить еще одно выравнивание по семи точкам:

 

И в заключение

В результате мы должны будем получить выражение (4.31).

Чем вызвано применение скользящих средних Спенсера в методе Шискина—Эйзенпресса? Дело в том, что скользя­щая средняя с симметрично-равными весами вида (4.22) по­зволяет выделить лишь линейный тренд. Если же тренд на самом деле не линеен, то сглаживание временного ряда, содер­жащего нелинейный тренд, дает искаженные его значения. Скользящая средняя Спенсера позволяет получать точные оценки тренда, выраженного полиномами до третьей степени включительно.

Рассмотрим теперь собственно метод Шискина—Эйзен­пресса.

1. Исходный ряд выравнивается скользящей средней (4.22). Делается это, как и в методе Четверикова, с той целью, чтобы не исказить сезонную компоненту Если бы мы ис­пользовали скользящую среднюю с другим периодом сколь­жения, то это привело бы к изменению как амплитуды, так и формы сезонной волны.

2. Рассчитываются остаточные значения:

или

 

Вычисляются средние значения остаточного ряда в целом по ряду и по месяцам (кварталам) :

 

 

3. Находится предварительная оценка средней сезонной волны

 

и строится новый ряд, относительно свободный от сезонной компоненты

 

4. К ряду применяется сглаживание скользящей средней Спенсера:

5. Находится улучшенная оценка сезонной компоненты:

 

Пример 1.Применим метод Четверикова для выделения компонент временного ряда, приведенного в табл. 4.6.

1. Проведем выравнивание эмпирического ряда {Y_t} cис­пользованием центрированной скользящей средней с перио­дом сглаживания .

Полученную предварительную оценку тренда вы­читаем из исходного эмпирического ряда

или

2. Вычисляем для каждого года i (по строке) среднеквадратическое отклонение величины , используя для этого формулу

 

 

 

Значения величин :

 

t
	1,22	1,29	1,60	1,54	2,00	1,63	1,38	1,83	1,82	1,69	1,67	1,90	5,55

 

При вычислении во внимание принимались только шесть последних уровней первого года: , а при вы­числении первые шесть уровней тринадцатого года:

Делим отдельные значения каждого месяца из табл. 4.6 на отклонения соответствующего года. В результате получаем табл. 4.7, в которой

3. Последняя строка табл. 4.7 представляет собой значе­ния предварительной средней сезонной волны, вычислен­ной по формуле:

Таблица 4.7. Нормированный остаточный ряд

 

Год	Месяц
	-1,48 -1,38 -2,04 -1,48 -1,42 -1,43 -1,96 -1,76 -1,53 -1,30 -1,41 -0,66	-1,85 -1,69 -1,18 -2,07 -1,85 -1,74 -2,62 -1,65 -1,99 -1,86 -2,02 -0,67	-0,49 -0,19 -0,25 -0,67 -0,42 -0,81 -0,70 -0,37 -0,31 -0,68 -0,01 -0,10	0,03 -0,04 0,27 -0,11 0,07 0,25 0,05 0,06 0,30 -0,11 0,03 -0,01	0,36 0,78 0,75 0,85 0,98 1,07 0,73 0,69 0,89 0,75 1,16 0,29	0,85 0,81 0,93 1,03 1,13 1,04 0,98 0,95 0,75 0,88 0,75 0,25	1,19 1,09 1,25 1,07 0,98 1,05 0,74 0,83 1,14 1,09 0,96 0,84	1,31 1,31 1,23 1,08 0,91 0,85 1,21 0,95 1,08 0,97 1,18 1,09	0,84 0,54 0.36 0,70 0,39 0,51 0,92 0,85 0,40 0,49 0,83 0,89	0,43 0,73 0,50 0,64 0,24 0,24 0,44 0,27 0,36 0,42 0,41 0,17	-0,79 -0,31 -0,78 0,01 -0,32 -0,43 -0,25 -0,33 -0,32 -0,22 -0,77 -0,26	-0,65 -0,67 -0,94 -0,84 -0,54 -0,90 -0,24 -0,31 -0,90 -0,79 -0,50 -0,55
	-1,49	-1,68	-0,42	0,07	0,78	0,86	1,02	1,10	0,64	0,40	-0,40	-0,65

4. Предварительную среднюю сезонную волну умно­жаем на среднеквадратическое отклонение каждого года a_t и вычитаем из исходного эмпирического ряда:

 

В результате получаем ряд, лишенный предварительной сезонной волны (табл. 4.8).

Таблица 4.8.

Год	Месяц
	10,42 11,78 11,13 12,13 13,31 13,92 13,57 14,90 15,73 16,57 17,56 22,56	10.28 11,69 12,77 11,38 12,98 13,79 14,62 15,54 15,30 16,00 16,85 23,64	10,47 12,11 12,29 11,71 13,31 13,39 14,08 15,60 16,04 15,96 18,39 19,83	10,61 11,62 12,38 11,87 13,39 14,24 14,65 15,52 16,28 16,18 17,61 17,71	10,23 11,80 12,08 12,40 13,76 14,46 14,65 15,43 16,12 16,48 18,49 15,49	10,87 11,71 12,31 12,67 13,93 14,42 15,03 15,75 15,81 16.63 17,65 13,94	10,21 11,06 12,11 12,31 12,37 13,58 13,81 14,54 15,83 16,17 16,61 17,50	10.34 11,31 11,98 12,13 12,25 13,23 14,31 14,71 15,62 15,90 16,87 17,86	10,42 11,01 11,39 12,12 12,28 13,47 14,58 15,48 15,23 15,89 17,18 18,36	10,28 11,67 12,05 12,34 12,59 13,47 14.28 14,95 15,64 16,17 17,03 17,47	9,83 11,49 11,22 12,63 13,20 13,74 14,48 15,40 15,92 16,46 16,54 18,17	10,34 11,47 11,49 11,75 13,35 13,41 14,90 15,94 15,35 15.96 17,56 18.11

5. Временной ряд, лишенный предварительной сезон­ной волны, сглаживаем с использованием простой скользя­щей средней с интервалом сглаживания, равным пяти, и получаем новую оценку тренда (табл. 4.9).

Таблица 4.9. Новая оценка

Год	Месяц
	10,27 11,71 11,78 11,92 13,23 13,65 14,33 15,48 15,67 16,19 17,38 20,46	10,42 11,73 12,02 11,79 13,27 13,75 14,36 15,50 15,74 16,13 17,59 20,37	10,40 11,80 12,13 11,90 13,35 13,96 14,31 15,40 15,89 16,24 17,78 19,85	10,49 11,79 12,37 12,01 13,43 14,06 14,61 15,57 15,91 16,25 17,80 18,12	10,65 11,87 12,27 12,20 13,59 14,06 14,59 15,63 16,08 16,37 17,93	10,82 11,84 12,24 12,31 13,58 14,25 14,72 15,63 16,06 16,55 17,82	10,90 11,80 12,19 12,39 13,59 14,32 14,88 15,57 15,98 16,75 17,97	11,18 11,85 12,24 12,43 13,54 14,28 14,94 15,61 15,99 16,86 17,77	10,22 11,31 11,75 12,31 12,54 13,50 14,29 15,02 15,65 16,12 16,85 17,87	10,24 11,39 11,63 12,19 12,73 13,46 14,51 15,30 15,55 16,08 17,04 17,99	10,26 11,48 11,46 12,19 12,95 13,60 14,36 15,33 15,57 16,21 17,17 18,93	10,23 11,62 11,73 12,05 13,09 13,67 14,37 15,35 15,59 16,23 17,11 19,99

 

6. Вычисляем отклонения ряда от исходного эмпирического ряда

Полученные отклонения подвергаем обработке в соответ­ствии с пп. 2 и 3 для выявления новых значений сезонной волны. Получаем следующие значения:

t
	-1,54	-1,81	-0,43	0,08	0,82	0,93	1,01	1,09	0,63	0,41	-0,40	-0,72

 

При сравнении значений коэффициентов сезонной вол­ны, полученных на первой и второй итерациях, т. е. значе­ний и , нетрудно заметить, что они незначительно отличаются друг от друга.

7. Производим вычисление коэффициента напряженно­сти сезонной волны в следующем порядке: по формуле фактически получаем значения случайной компоненты, которые для нашего примера приведены в табл. 4.10.

Таблица 4.10. Вычисление значений случайной компоненты

Год	Месяц
	-0,23 -0,77 -1,40 -1,23 -0,81 -0,25 -1,95 -1,75 -0,92 -0,57 -1,13	-0,50 -0,92 -0,02 -1,96 -1,22 -0,47 -1,00 -1,21 -1,47 -1,13 -2,12	-0,04 0,07 -0,06 -0,60 -0,29 -0,72 -0,57 -0,13 -0,13 0,56 0,24	0,13 -0,14 0,04 -0,08 -0,05 0,20 0,09 0,00 0,41 -0,03 -0,14	-0,23 0,36 0,13 0,94 0,62 0,66 0,67 0,40 0,54 0,59 1,22	0,23 0,32 0,46 1,15 0,82 0,43 0,95 0,76 0,27 0,59 0,53	0,47 0,93 0,68 1,01 0,64 -0,11 0,52 1,11 0,90 0,55 0,46	0,46 0,80 0,49 0,93 0,39 0,46 0,69 0,92 0,68 0,76 1,09	-0,10 0,03 0,17 0,39 0,38 0,54 1,00 0,11 0,22 0,77 1,08	0,39 0,65 0,36 0,25 0,25 -0,09 -0,03 0,41 0,36 0,25 -0,17	-0,11 -0,48 -0,22 0,15 -0,11 -0,03 0,26 0,02 -0,03 -0,90 -1,12	-0,27 -0,56 -0,58 -0,32 -0,60 0,35 0,12 -0,70 -0,65 0,08 -2,40

 

С использованием соотношения

 

определяем величины коэффициента напряженности K_t для каждого года, кроме первого и последнего. Для первого и последнего годов значение коэффициента напряженности не вычисляются, так как после повторного сглаживания в них ос­талось лишь по четыре наблюдения, и их использование иска­жает при расчетах средние характеристики всего ряда.

Значения коэффициента напряженности сезонной волны:

 

t
	3,02	2,47	2,44	2,09	2,48	2,48	2,41	2,10	2,34	2,08	1,79

 

8. Используя коэффициент напряженности Ки вычисляем окончательные значения сезонной компоненты временного ряда (табл. 4.11):

Перейдем к рассмотрению статистических методов оценки уровня сезонности. До сих пор мы в основном использовали аддитивное представление модели сезонного временного ряда (4.19). Однако не менее разумной, как считают многие спе­циалисты, является и мультипликативная модель:

где «годовая» составляющая (тренд);

постоянная пропорциональности для го месяца (квартала), не меняющаяся от года к году.

Поскольку постоянная пропорциональности безразмер­ная и не меняется от года к году, то ее можно использовать для определения уровня сезонности во временном ряду.

Таблица 4.11. Сезонная компонента временного ряда

 

-4,65 -3,80 -3,73 -3,22 -3,82 -3,82 3,71 -3,23 -3,60 -3,20 -2,76	-5,47 -4,47 -4,42 -3,78 -4,49 -4,49 -4,36 -3,80 -4,24 -3,76 -3,24	-1,30 -1,01 -1,04 -0,90 -1,07 -1,07 -1,04 -0,90 -1,01 -0,89 -0,77	0,24 0,20 0,20 0,17 0,20 0,20 0,19 0,17 0,19 0,17 0,14	2,48 2,03 2,00 1,71 2,03 2,03 1,98 1,72 1,92 1,71 1,47	2,81 2,30 2,27 1,94 2,31 2,31 2,24 1,95 2,18 1,93 1,66	3,05 2,49 2,46 2,11 2,50 2,51 2,43 2,12 2,36 2,10 1,81	3,29 2,69 2,66 2,28 2,70 2,70 2,63 2,29 2,55 2,27 1,95	1,90 1,56 1,52 1,25 1,56 1,56 1,52 1,32 1,47 1,31 1,13	1,24 1,01 1,00 0,86 1,02 1,02 0,99 0,86 0,96 0,85 0,73	-1,21 -0,99 -0,96 -0,84 -0,99 -0,99 -0,96 -0,84 -0,94 -0,83 -0,72	-2,17 -1,78 -1,76 -1,50 -1,78 -1,79 -1,74 -1,51 -1,68 -1,50 -1,29

 

Приближенные оценки коэффициентов пропорциональ­ности могут быть получены следующим образом

 

где

и

Если известны значения тренда и сезонной компо­ненты в аддитивной модели, то можно оценить и более точно:

 

 

Последнее говорит о возможности оценки уровня сезон­ности независимо от того, какая рассматривается модель: (4.19) или (4.40). Оценки ,по формуле (4.41) иногда назы­вают еще индексами сезонности.

Чаще, однако, рассматривают не просто ряд из относи­тельных величин ,а ряд процентов:

 

.

 

Из (4.44) с учетом (4.43) можно заключить, что индексы сезонности ,характеризуют степень отклонения уровня се­зонного временного ряда от ряда средних (тренда) или, иначе говоря, степень колеблемости относительно 100%, так как если ,то .

Пример 2.Найдем оценки уровня сезонности временно­го ряда, представленного в табл. 4.6, через индексы сезонно­сти, проводя расчет по формуле (4.43). Для этого восполь­зуемся табл. 4.9, 4.11, в которых приведены значения трен­да и сезонной компоненты . В результате получим табл. 4.12, состоящую из коэффициентов .

Таблица 4.12

Год	Месяц
	0,55 0,68 0,68 0,73 0,71 0,72 0,74 0,79 0,77 0,80 0,84	0,48 0,62 0,63 0,68 0,66 0,67 0,70 0,75 0,73 0,77 0,82	1,88 0,91 0,91 0,92 0,92 0,92 0,93 0,94 0,94 0,95 0,96	1,02 1,02 1,02 1,01 1,01 1,01 1,01 1,01 1,01 1,01 1,01	1,23 1,17 1,16 1,14 1,15 1,14 1,14 1,11 1,12 1,10 1,08	1,26 1,19 1,19 1,16 1,17 1,16 1,15 1,12 1,14 1,12 1,09	1,28 1,21 1,20 1,17 1,18 1,18 1,16 1,14 1,15 1,13 1,10	1,29 1,23 1,22 1,18 1,20 1,19 1,18 1,05 1,16 1,13 1,11	1,17 1,13 1,12 1,10 1,12 1,10 1,10 1,08 1,09 1,08 1,06	1,11 1,09 1,08 1,07 1,08 1,07 1,06 1,06 1,06 1,05 1,04	0,89 0,19 0,92 0,94 0,93 0,93 0,94 0,95 0,94 0,95 0,96	0,81 0,85 0,85 0,89 0,87 0,88 0,89 0,90 0,90 0,91 0,94
	8,01	7,51	10,18	11,14	12,54	12,75	12,90	13,04	12,15	11,77	10,26	9,69
, %	72,80	68,30	92,50	101,3	114,0	115,9	117,3	118,5	110,5	107,0	93,3	88,1

 

В предпоследней строке табл. 4.12 приведены суммы по столбцам, в последней строке — индексы сезонности .

Таким образом, в 1-м, 2-м, 3-м и 11-м, 12-м месяцах уро­вень временного ряда меньше значений тренда, а в 4-м — 10-м этот уровень больше значений тренда.

Таким образом, в изучаемом экономическом явлении (объем перевозок морским транспортом) явно присутствует сезонная составляющая с пиком в летние месяцы. Количе­ственную характеристику этой сезонности дает сезонная волна в виде совокупности индексов сезонности, представ­ленных в последней строке табл. 4.12.

Вопросы и задания

1. Дайте определение временного экономического ряда и характеристику его структурно образующих элементов.

2. Что такое аномальный уровень временного ряда? Какие методы обнаружения и устранения аномальных уровней вы знаете?

3. Перечислите основные этапы изученных методов опре­деления наличия тренда.

4. Поясните суть методов механического сглаживания вре­менных рядов. Дайте сравнительную характеристику этих методов.

5. Назовите основные показатели экономической динами­ки, рассчитываемые на основе временных рядов.

6. В чем сущность явления автокорреляции во временных рядах? Что такое временной лаг?

7. Дайте характеристику явления сезонности в экономиче­ских процессах. Какие методы выявления и фильтра­ции сезонной компоненты временного ряда вы знаете?

8. Поясните суть статистических методов анализа сезонно­сти. Что такое сезонная волна?