Виды систем уравнений в эконометрике. Структурная и приведенная формы модели.

Для изучения комплексных экономических явлений средствами эконометрики, как правило, применяют не отдельные уравнения регрессии, а системы уравнений. Это объясняется следующим:

1. Описывая явление с помощью взаимосвязанных переменных, приходится учитывать, что изменение одной переменной влечет за собой изменение других. При рассмотрении же отдельного регрессионного уравнения часто предполагают, что объясняющие переменные можно изменять независимо одну от другой.

2. Взаимодействие переменных нередко затрудняет однозначную их классификацию при построении модели: одну и ту же переменную можно определить как объясняющую (фактор) и как объясняемую (результат).

Системы уравнений в эконометрике подразделяют на виды: независимых уравнений, рекурсивных уравнений и взаимозависимых (совместных) уравнений.

Системы совместных уравнений, представляет наибольший практический интерес. Такие системы эффективны в эконометрических исследованиях и наиболее широко применяются в макроэкономике. В силу этого под системой эконометрических уравнений обычно понимают систему совместных уравнений. Систему совместных (взаимозависимых) уравнений называют системой одновременных уравнений, указывая на то, что одни и те же переменные системы рассматриваются одновременно как объясняемые в одном уравнении и как объясняющие — в остальных уравнениях.

Ø система независимых уравнений (1), когда каждый результативный признак (объясняемая переменная) y_j , где 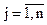является функцией одной и той же совокупности факторов (объясняющих переменных) x_j , где 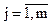. Набор факторов в каждом уравнении системы может варьировать в зависимости от изучаемого явления

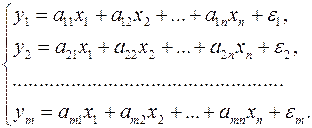(1)

Каждое уравнение системы независимых уравнений может рассматриваться самостоятельно. Для нахождения его параметров используется метод наименьших квадратов. Каждое уравнение этой системы является уравнением регрессии. Т. к. фактические значения зависимой переменной отличаются от теоретических на величину случайной ошибки, то в каждом уравнении присутствует величина случайной ошибки .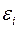

Ø система рекурсивных уравнений (2),когда результативный признак y_j где 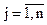одного уравнения системы в каждом последующем уравнении является фактором наряду с одной и той же совокупностью факторов x_j , где .

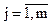(2)

Каждое уравнение этой системы может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов (МНК).

Ø Система одновременных уравнений, когда результативный признак y_j, где 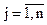одного уравнения системы входи во все другие уравнения системы в качестве фактора наряду с одной и той же совокупностью факторов x_j , где 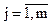. Модели системы одновременных уравнений могут быть представлены в виде структурной формы модели или в виде приведенной формы модели. Основными составляющимиобеих форм записи являются эндогенныеи экзогенные переменные. Эндогенные переменные (у) определяются внутри модели и являются зависимыми переменными. Экзогенные переменные (х) определяются вне системы и являются независимыми переменными. Предполагается, что экзогенные переменные не коррелируют с ошибкой в соответствующем уравнении.

Зависимые переменные в одних уравнениях модели входят в левую часть, а в других уравнениях – в правую часть системы:

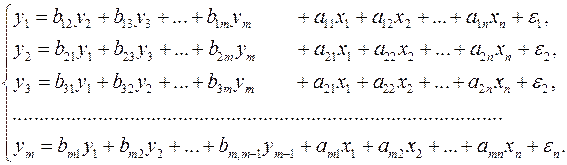(3)

Каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим. С этой целью используются специальные приемы оценивания.

Система одновременных уравнений может быть представлена в виде структурной формы модели или приведенной формы модели

Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные.

Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, а в других как экзогенные переменные. Внеэкономические переменные (например, климатические условия, социальное положение, пол, возрастная категория) входят в систему только как экзогенные переменные. В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (лаговые переменные).

Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных.

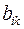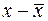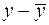Структурная форма модели в правой части содержит при эндогенных переменных коэффициенты и экзогенных переменных – коэффициенты , которые называются структурными коэффициентами модели. Все переменные в модели выражены в отклонениях от среднего уровня, т.е. под подразумевается , а под – соответственно . Поэтому свободный член в каждом уравнении системы (3) отсутствует.

Использование МНК для оценивания структурных коэффициентов модели дает смещенные и несостоятельные оценки. Для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.

Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:

(4)

где – коэффициенты приведенной формы модели, 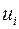– остаточная величина для приведенной формы.

По своему виду приведенная форма модели ничем не отличается от системы независимых уравнений, параметры которой оцениваются традиционным МНК. Применяя МНК, можно оценить , а затем оценить значения эндогенных переменных через экзогенные.

Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели.

Пример: модель динамики цены и заработной платы вида для структурной модели вида

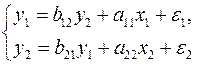(5)

где 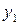- темп изменения месячной заработной платы;

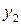- темп изменения цен;

- процент безработных;

- темп изменения постоянного капитала;

- темп изменения цен на импорт сырья.

приведенная форма модели имеет вид

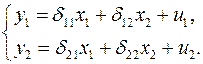(6)

Из первого уравнения (5) можно выразить 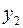следующим образом (для упрощения уравнения случайная величина не показана):

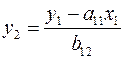Подставляя во второе уравнение (5), имеем

откуда

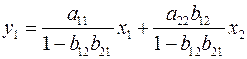Поступая аналогично со вторым уравнением системы (5), получим

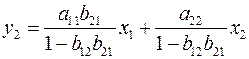т.е. система (5) принимает вид

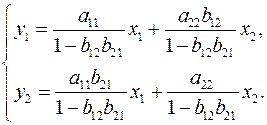
Таким образом, можно сделать вывод о том, что коэффициенты приведенной формы модели будут выражаться через коэффициенты структурной формы следующим образом:

Приведенная форма модели позволяет получить значения эндогенной переменной через значения экзогенных переменных, но аналитически она уступает структурной форме модели, так как в ней отсутствуют оценки взаимосвязи между эндогенными переменными.