Отбор факторных признаков при построении множественной регрессии.

Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Он включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии.

Отбор факторов является важнейшей проблемой при построении множественных регрессионных моделей. Он проводится на основе качественного и количественного анализа социально-экономических явлений с использованием статистических и математических критериев.

Проводят три стадии отбора факторов.

1. Предварительное определение перечня факторов, оказывающих влияние на переменную у

2. Сравнительная оценка и отсев факторов

3. Окончательный отбор факторов в процессе построения разных вариантов моделей и оценки значимости их параметров

Для сравнительной оценки и отсева части факторов составляют матрицу парных коэффициентов корреляции, измеряющих тесноту линейной связи каждого фактора с результативным признаком и с каждым из остальных факторных признаков (таблица 43).

Матрица парных коэффициентов корреляции — симметричная матрица (r_ij = r_ji.) , на главной диагонали которой расположены характеристики силы связи признаков с самими собой, все другие элементы являются парными коэффициентами корреляции i-го и j-го признаков.

Корреляционная матрица позволяет выявить факторы, которые находятся в тесной линейной корреляционной взаимосвязи, близкой к функциональной (таблица 43).

Таблица 43 - Корреляционная матрица.

	y	x₁	x₂	…	x_j	…	x_k
y		r_yx1	r_yx2	…	r_yx2	…	r_yxk
x₁	r_x1y		r_x1x2	…	r_x1xj	…	r_x1xk
x₂	r_x2y	r_x2x1		…	r_{x2 xj}	…	r_x2xk
…	…	…	…	…	…	…	…
x_j	r_xjy	r_xjx1	r_xjx2	…		…	r_xjxk
…	…	…	…	…	…	…	…
x_k	r_xky	r_xkx1	r_xkx₂	…	r_xkxj	…

где y – результативный признак;

x_1, x_2,…, x_k – факторные признаки;

r_ij – парный коэффициент корреляции между признаками x_i и x_j_.

Если в модель включаются два или более тесно взаимосвязанных фактора, то наряду с уравнением регрессии появляется и другая линейная зависимость. Подобное явление, называемое мультиколлинеарностью. Мультиколлинеарность – тесная зависимость между факторными признаками, включенными в модель.

Мультиколлинеарность искажает величину коэффициентов регрессии, затрудняет их экономическую интерпретацию.

Изменения, возникающие под воздействием мультиколлинеарности.

Ø Искажает величины параметров модели, которые имеют тенденцию к завышению.

Ø Приводит к изменению смысла экономической интерпретации коэффициентов регрессии.

Ø Вызывает слабую обусловленность системы нормальных уравнений.

Ø Осложняет процесс определения наиболее существенных факторных признаков

Решение проблемы мультиколлинеарности

В решении проблемы мультиколлинеарности можно выделить несколько этапов.

1. Установление наличия мультиколлинеарности.

2. Определение причин возникновения мультиколлинеарности.

3. Разработка мер по устранению мультиколлинеарности.

Причины возникновения мультиколлинеарности между признаками.

Ø Изучаемые факторные признаки характеризуют одну и ту же сторону явления или процесса (например, показатели объема произведенной продукции и среднегодовой стоимости основных фондов одновременно включать в модель не рекомендуется, так как оба характеризуют размер предприятия)

Ø Использование в качестве факторных признаков, суммарное значение которых представляет собой постоянную величину (например, коэффициент годности и коэффициент износа основных фондов)

Ø Факторные признаки, являющиеся элементами друг друга (например, затраты на производство продукции и себестоимость единицы продукции)

Ø Факторные признаки, по экономическому смыслу дублирующие друг друга (например, прибыль и рентабельность продукции)

Способы определения наличия или отсутствия мультиколлинеарности.

Ø Анализ матрицы коэффициентов парной корреляции

Факторы x_i и x_j могут быть признаны коллинеарными, если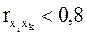

Ø Иследование матрицы X ́X.

Если определитель матрицы X ́X близок к нулю, то это свидетельствует о наличии мультиколлинеарности.

Устранение мультиколлинеарности возможно посредством исключения из корреляционной модели одного или нескольких линейно связанных факторных признаков или преобразование исходных факторных признаков в новые, укрупненные факторы. Вопрос о том, какой из факторов следует отбросить, решается на основе качественного и логического анализа изучаемого явления.

Методы устранения или уменьшения мультиколлинеарности

1. Сравнение значений линейных коэффициентов корреляции

При отборе факторов предпочтение отдается тому фактору, который более тесно, чем другие факторы, связан с результативным признаком, причем желательно, чтобы связь данного факторного признака с у была выше, чем его связь с другим факторным признаком, т.е.

2. Метод включения факторов.

Метод заключается в том, что в модель включаются факторы по одному в определенной последовательности. На первом шаге в модель вводится тот фактор, который имеет наибольший коэффициент корреляции с зависимой переменной.

На втором и последующих шагах в модель включается фактор, который имеет наибольший коэффициент корреляции с остатками модели. После включения каждого фактора в модель рассчитывают ее характеристики, и модель проверяют на достоверность.

3. Метод исключения факторов

Метод состоит в том, что в модель включаются все факторы. Затем после построения уравнения регрессии из модели исключают фактор, коэффициент при котором незначим и имеет наименьшее значение t-критерия. После этого получают новое уравнение регрессии и снова проводят оценку значимости всех оставшихся коэффициентов регрессии.

Процесс исключения факторов продолжается до тех пор, пока модель не станет удовлетворять определенным условиям и все коэффициенты регрессии не будут значимы.

Пример17:

Требуется провести отбор факторов в модель множественной регрессии на основе условных исходных матрицы парных коэффициентов корреляции (таблица 44):

Таблица 44 – Отбор факторов в модель множественной регрессии.


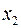
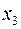
	0,8	0,7	0,6
0,8		0,8	0,5
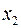
0,7	0,8		0,2
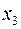
0,6	0,5	0,2

Решение:

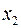Очевидно, что факторы и дублируют друг друга. Корреляция 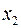с результатом слабее, чем корреляция фактора с 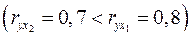, но значительно слабее межфакторная корреляция 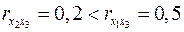. Исходя из проведенного исследования в анализ целесообразно включить фактор 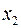, а не . В уравнение множественной регрессии включаются факторы 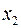, .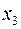