Попарное сравнение объектов

Пример

Пусть S = 2, n = 3 и матрица экспертных оценок равна

Как видно, первый и второй эксперты важность обоих объектов оценивают одинаково, причем второй объект признается заметно более важным, чем первый (0,8 против 0,2). Третий эксперт по какой-то причине (некомпетентность, предвзятость и т.п.) придерживается противоположного мнения.

Определим коэффициенты компетентности экспертов и вычислим усредненные (с учетом компетентности) оценки важности объектов.

По формуле (9) рассчитаем матрицу взаимосвязи экспертных оценок

 

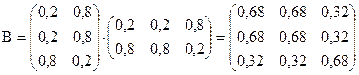
Имеем и по формуле (8) получим

Для определения нормирующего множителя используем уравнение

 

Следовательно

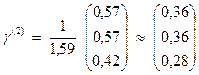
По формуле (6) находим

 

Для k = 3 из (8) получим

 

 

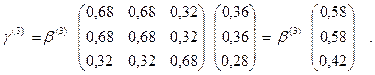
Отсюда Таким образом

Дальнейшие вычисления приводят к практически идентичным результатам.

 

 

Часто трудно оценить важность некоторого объекта среди ряда других – например, при анализе объектов различной природы. Среди ранжируемых показателей эффективности могут быть показатели со стоимостным выражением, показатели этического, эстетического рода и т.п. Это затруднение устраняется путем попарного сравнения объектовпо степени их влияния на достижение цели. Эксперт должен вынести суждение о том, насколько с точки зрения достижения цели один объект важнее второго. Анализируя совокупность объектов, он определяет численное предпочтение одного объекта перед другим по некоторой заранее выбранной шкале. Примером может служить выбор места работы выпускником ВУЗа, который должен оценить, насколько для него уровень оплаты труда, важнее, чем перспективы продвижения по служебной лестнице и т.д.

Пусть эксперт анализирует объектов. Сравнивая их попарно между собой, он определяет чисел , характеризующих относительную значимость 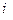- го объекта по сравнению с - м. Величина представляет оценку (приближенное значение) истинной значимости 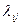сравниваемых объектов. Совокупность экспертных оценок записывают в виде квадратной матрицы

,

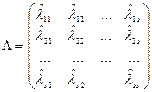элементы которой (относительные значимости объектов) можно рассматривать как отношения истинных важностей

(15.10)

При оценке относительных значимостей используется девятибалльная шкала

относительной важности объектов.

 

Степень важности	Определение	Пояснения
	Объекты одинаково важны	Оба объекта вносят одинаковый вклад в достижение цели
	Один объект немного важнее другого	Есть основания предпочесть один объект другому, но их нельзя считать неопровержимыми
	Один объект существенно важнее другого (сильное превосходство)	Существуют веские свидетельства того, что один из объектов более важен
	Один объект явно важнее другого	Имеются неопровержимые свидетельства превосходства одного объекта над другим
	Один объект абсолютно важнее другого	Превосходство одного объекта над другим не вызывает сомнения
2, 4, 6, 8	Значения, приписываемые промежуточным суждениям	Используются, когда выбор между двумя соседними нечетными числами затруднителен

 

Из формулы (10) следует, что из общего числа всех элементов матрицы независимы лишь . Во-первых, диагональные элементы равны единице. Во-вторых, при изменении порядка сравнения оценка относительной значимости объекта должна меняться на обратную

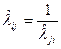, (15.11)

т.е. элементы, симметричные относительно главной диагонали, являются взаимно обратными числами.

Чрезвычайно важным является требование транзитивной согласованностиэлементов матрицы 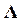, которое означает, что должны выполняться условия

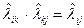, (15.12)

которые могут быть получены из формулы (15.10).

Матрица попарного сравнения объектов, элементы которой удовлетворяют условиям (10)-(12), называется согласованной. Следует отметить, что при попарном сравнении объектов эксперту не всегда удается выполнить условие транзитивной согласованности. В принципе, допускается некоторая степень несогласованности матрицы попарных сравнений.

По матрице попарного сравнения , составленной экспертом, легко могут быть оценены важности объектов . Используя (10) легко показать, что в случае согласованной матрицы справедливы соотношения: ……

Пример. Матрица попарных сравнений имеет вид:

Легко убедиться в том, что данная матрица удовлетворяет условиям согласованности; расчет дает .

Если матрица не является согласованной, то вектор оценок вычисляют как нормированный собственный вектор матрицы , соответствующий ее наибольшему собственному числу. Расчеты подобного рода проводятся рекуррентно.