Усреднение экспертных оценок
Пусть экспертам необходимо сравнить 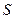 объектов. Предположим, что существует набор чисел
объектов. Предположим, что существует набор чисел  , характеризующих истинные значения важности этих объектов и неизвестных экспертам и ЛПР. Наиболее важному объекту соответствует наибольшее, а наименее важному – наименьшее число из
, характеризующих истинные значения важности этих объектов и неизвестных экспертам и ЛПР. Наиболее важному объекту соответствует наибольшее, а наименее важному – наименьшее число из  . Так как ранжирование объектов по важности определяется относительнымивеличинами чисел
. Так как ранжирование объектов по важности определяется относительнымивеличинами чисел  , то будем считать, что
, то будем считать, что

Пусть важность объектов оценивают  экспертов. Обозначим через
экспертов. Обозначим через  оценку важности
оценку важности 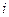 - го объекта
- го объекта 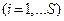 , данную
, данную  - м экспертом
- м экспертом 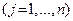 . Полученные оценки представим в виде матрицы
. Полученные оценки представим в виде матрицы
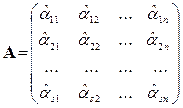 , (15.1)
, (15.1)
число строк которой соответствует числу объектов, а число столбцов – числу экспертов. Поскольку оценки важности одного и того же объекта разными экспертами могут не совпадать (числа в строках, вообще говоря, различны), то возникает задача определения показателей важности 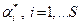 , представляющих усредненное мнение всех экспертов.
, представляющих усредненное мнение всех экспертов.
Усредненные показатели важности рассчитываются по формулам:
 (15.2)
(15.2)
причем 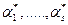 удовлетворяют условию нормировки
удовлетворяют условию нормировки
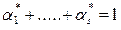 .
.
Таким образом, относительные оценки важности вычисляются как среднеарифметические оценок, выставленных всеми экспертами. Данный простейший подход применяется тогда, когда ЛПР уверен в одинаковой компетентности и объективности экспертов.
При различных уровнях компетентности экспертов вводятся коэффициенты компетентности экспертов 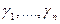 , отвечающие условиям:
, отвечающие условиям:
 (15.3)
(15.3)
При этом формула (2) обобщается и принимает вид

Представим последнее равенство в матричной форме. Для этого введем векторы-столбцы

где символ  обозначает операцию транспонирования. В результате формула (4) примет вид:
обозначает операцию транспонирования. В результате формула (4) примет вид:

При известной компетентности экспертов расчет усредненных оценок важности проводится по формулам (4) или (5).
Более сложным и реалистическим является случай, когда коэффициенты компетентности неизвестны. При этом используется рекуррентный метод расчета.
Обозначим через 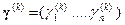 вектор коэффициентов компетентности на
вектор коэффициентов компетентности на  - м шаге вычислений
- м шаге вычислений 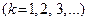 . Примем, что на первом шаге
. Примем, что на первом шаге
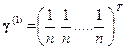 .
.
Для  - го шага оказываются справедливыми соотношения
- го шага оказываются справедливыми соотношения
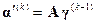 (15.6)
(15.6)
 , (15.7)
, (15.7)
где  - нормирующий множитель, вычисляемый из условия
- нормирующий множитель, вычисляемый из условия
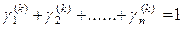 .
.
Подставляя (6) в (7) получим соотношение
 (8)
(8)
где квадратная симметрическая матрица  определяется равенством
определяется равенством

и называется матрицей взаимосвязи экспертных оценок.