Принцип оптимальности Беллмана и алгоритм решения задач динамического программирования

Необходимые условия применения метода ДП:

Ø объект исследования - управляемая система с заданными допустимыми состояниямии управлениями;

Ø задача может интерпретироваться как многошаговый процесс, каждый шаг включает принятие решенияо выборе одного из управлений;

Ø состояние, в котором оказывается система после выбора решения на k-м шаге, зависит только от данного решения и состояния к началу k-гошага. Это свойство называется отсутствием последействия.

Важно понимать, что в ДП речь не идет о простой оптимизации каждого шага управления независимо от других шагов. Шаговое управление должно проводиться дальновидно, с учетом последствий в будущем. Т.е. управление на i-м шаге выбирается не так, чтобы выигрыш именно на данном шаге был максимален, а так, чтобы была максимальна сумма выигрышей на всех оставшихся до конца шагах, включая данный.

Более строго это положение формулирует принцип оптимальности Беллмана, лежащий в основе метода ДП:

Каково бы ни было состояние системы S перед очередным шагом, надо выбирать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным.

Важно, что среди всех шагов есть один, который можно планировать без учета его последствий. Это - последний шаг, который может быть выбран так, чтобы он принес наибольшую выгоду.

В связи с этим, процесс ДП обычно проводится в направлении от конца к началу, т.е. планируется сначала последний шаг . При этом делаются различные предположения о том, чем кончился предпоследний -й шаг, и для каждого из этих предположений находится условное оптимальное управление на -м шаге («условное» означает, что управление выбирается исходя из условия, что предпоследний шаг закончился каким-то конкретным образом). После этого процесс продолжается. Проводится оптимизация управления на предпоследнем ()-м шаге с учетом всех возможных предположений об окончании ()-го шага и т.д. вплоть до первого шага.

После определения условно оптимальных управлений на всех шагах определяется оптимальное управление для всего процесса.

Алгоритм использования метода ДП:

1. Выбираются параметры состояния управляемой системы;

2. Операция расчленяется на этапы;

3. Определяется набор шаговых управлений ;

4. Определяется, какой выигрыш приносит на i-м шаге управление , если перед этим система была в состоянии i-1 (), т.е. записывается “функция выигрыша”:

5. Определяется, как изменяется состояние системы под влиянием управления на i-м шаге

(переход системы из состояния в состояние 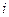; при этом должны быть определены «функции изменения состояния» (19.5));

6. Записывается основное рекуррентное соотношение ДП (уравнение Беллмана), выражающее условный оптимальный выигрыш (начиная с 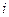-го шага и до конца) через уже известную функцию :

Этому выигрышу соответствует условное оптимальное управление на i-м шаге;

7. Производится условная оптимизация последнего (-го шага) по формуле

и определяется соответствующее условное оптимальное управление;

8. Производится условная оптимизация ()-го, ()-го, и т.д. шагов по формуле (6), полагая в ней и т.д. и для каждого из шагов определяется условное оптимальное управление;

9. Производится безусловная оптимизация путем перемещения в прямом направлении – от первого шага к последнему

Рассмотрим использование метода ДП на примере.

Пример 1. Имеется управляемая система, которая может под влиянием управления переходить из данного состояния в одно из двух соседних состояний. С переходами связаны некоторые затраты. Требуется перевести систему из начального состояния в конечное при минимальных совокупных затратах (Рис. 19.1).

Рис. 19.1.

Любой полный путь состоит из 5+7=12 шагов. Состояние системы перед каждым шагом характеризуется двумя координатами – “восточной” и “северной”. Для каждого из состояний системы нужно найти условное оптимальное управление (перемещаться “на север” или “на восток”). Управление выбирается так, чтобы стоимость всех оставшихся до конца шагов (включая данный) была минимальна. Эту стоимость назовем “условным оптимальным выигрышем” для данного состояния системы перед началом очередного шага.

Произведем оптимизацию последнего 12 шага. Рассмотрим правый верхний угол рис. 1. После 11 шага система может находиться лишь в одном из состояний (точек) . Если система оказалась в состоянии , то выбор отсутствует – требуется “идти на восток”, что потребует 10 д.е. Запишем число 10 в соответствующем кружке и обозначим оптимальное управление стрелкой. Для точки управление также вынужденное и затраты равны 14 д.е. Таким образом, проведена условная оптимизация последнего шага и найден условный оптимальный выигрыш для состояний и .

Проведем оптимизацию предпоследнего (11-го) шага. После предпоследнего (10-го) шага система могла оказаться в одном из трех состояний . Найдем для каждого из них условное оптимальное управление и условный оптимальный выигрыш. Для точки С1 управление вынужденное и требует 21 д.е. затрат (11+10).

Для состояния С2 управление уже не вынужденное – имеется два варианта, для первого требуется 28 д.е. (14+14), для второго - лишь 23 д.е. (13+10). Таким образом, для состояния С2 условное оптимальное управление – “идти на север”. Для точки С3 управление снова вынужденное и требует 22 д.е (8+14).

Продолжая вычисления, можно найти для каждого состояния условное оптимальное управление, обозначая его стрелками и условный оптимальный выигрыш, записываемый в кружки. Расход на данном шаге складывается с уже оптимизированным расходом, записанным в кружке, куда ведет стрелка. Таким образом, на каждом шаге оптимизируется только этот шаг, а следующие за ним уже оптимизированы. Конечный результат показан на Рис. 19.2.

Рис. 19.2.

Таким образом, условная оптимизация завершена, и в каком бы состоянии ни оказалась система, известно, как проводить процесс управления (по стрелке) и во что обойдется путь до конечного состояния (число в кружке).

Как видно из Рис. 19.2, минимальные затраты на перевод системы из начального в конечное состояние составляют 118 д.е.

Осталось построить безусловное оптимальное управление – траекторию, ведущую из начального в конечное состояние и требующую минимальных затрат. Для этого достаточно надлежащим образом двигаться вдоль стрелок.

Может возникнуть ситуация, когда оба управления для некоторого состояния являются оптимальными, т.е. приводят к одинаковому расходу средств от этого состояния до конечного. Например, для состояния (5;1), окрашенного в голубой цвет, оба управления являются оптимальными и требуют затрат 62 д.е. Из них можно выбрать любое, - от этого зависит оптимальное управление всем процессом, но не зависитоптимальный выигрыш.

Если решать задачу, выбирая на каждом шаге, начиная с первого, самое выгодное управление для этого шага, то получим затраты 128 д.е. (10+12+8+10+11+13+15+8+10+9+8+14), что существенно больше 118.