Сущность целочисленной оптимизации (целочисленного линейного программирования (ЦЛП))
Основные понятия и определения
В ЗАДАЧАХ ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ
Задачи целочисленной оптимизации. Частично целочисленные задачи. Дихотомические решения. Зависимые решения.
При решении многих оптимизационных задач требуется, чтобы компоненты вектора неизвестных 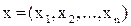 выражались в целых числах. В простейшем случае это может быть связано с необходимостью определения оптимального числа физически цельных объектов (станков, людей, транспортных единиц и т.д.). Задачи этого типа относятся к задачам целочисленной оптимизации или целочисленного линейного программирования (ЦЛП). Они требуют нахождения экстремума линейной целевой функции (критерия оптимальности)
выражались в целых числах. В простейшем случае это может быть связано с необходимостью определения оптимального числа физически цельных объектов (станков, людей, транспортных единиц и т.д.). Задачи этого типа относятся к задачам целочисленной оптимизации или целочисленного линейного программирования (ЦЛП). Они требуют нахождения экстремума линейной целевой функции (критерия оптимальности)

при ограничениях


Если требование целочисленности распространяется лишь на часть переменных, то задача называется частично целочисленной.
Задачи этого типа представляют отдельную область оптимизационного моделирования. Их роль в моделях принятия решений определяется тем, что они позволяют проводить выбор альтернатив для проблем высокой сложности.
Иногда решения задач ЦЛП получают, округляя результаты решений обычных задач линейного программирования. Например, если оптимальное число производимых станков крупным промышленным предприятием оказалось равным 3200,2, то в качестве оптимального решения соответствующей задачи целочисленной оптимизации берется округленное значение 3200.
Этот простой способ плохо работает при малых значениях переменных. Если решение обычной задачи линейной оптимизации предлагает произвести 3,6 крупных транспортных корабля класса А и 4,8 класса В, то округление этих значений до 4 и 5 соответственно может привести к нарушению ограничения по ресурсам.
Алгоритм округления не работает также в моделях, в которых переменные используются в качестве индикаторов логических решений. Пусть, например, переменная равна 1, если следует строить офис в некотором городе, и 0 - в противном случае. Значение решения, например, x = 0,38 не несет никакой полезной информации.
Целочисленность переменных существенно усложняет поиск оптимальных решений в случае большого числа переменных. Оптимизация моделей ЦЛП требует на 1-3 порядка больших затрат машинного времени по сравнению с задачами ЛП с тем же количеством переменных. Это связано с тем, что при решении задачи симплекс-методом решение ищется лишь в соответствующих вершинах многогранников, определяющих область допустимых решений (метод обхода), тогда как алгоритм решения задач ЦЛП требует расчета в гораздо большем числе точек. Это иллюстрируется рисунком, изображающим двумерную задачу; область допустимых решений (ОДР) схематически изображена затемненным пятиугольником.

Метод полного перебора (т.е. расчет значений ЦФ во всей области допустимых решений и выбор точки, соответствующей оптимальному значению) для большинства практических задач нереализуем. В случае, когда модель ЦЛП содержит 20 переменных, каждая из которых может принимать целые значения от 1 до 50, полный перебор требует провести 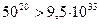 расчетов ЦФ и проверить принадлежность точек ОДР, что даже для современных суперкомпьютеров может потребовать многих лет непрерывной работы. Поэтому в компьютерных программах используются специально разработанные алгоритмы – например, метод ветвей и границ.
расчетов ЦФ и проверить принадлежность точек ОДР, что даже для современных суперкомпьютеров может потребовать многих лет непрерывной работы. Поэтому в компьютерных программах используются специально разработанные алгоритмы – например, метод ветвей и границ.
Во многих моделях ЦЛП переменные могут принимать только значения 0 или 1 (модели двоичного целочисленного линейного программирования). Эти модели особенно важны для ТПР, так как двоичные переменные можно использовать для представления дихотомических решений (решений типа “да – нет”). К этому классу задач принадлежат модели назначений, размещения производственных объектов и офисов, производственного планирования и управления инвестиционными портфелями.
Приведем два простых примера.
В модели размещения производственных объектов  , если принимается решение разместить завод в пункте j, и
, если принимается решение разместить завод в пункте j, и  , если решено завод в данном пункте не размещать.
, если решено завод в данном пункте не размещать.
В модели маршрутизации  , если дорога k ведет из пункта i в пункт j, и
, если дорога k ведет из пункта i в пункт j, и  в противном случае.
в противном случае.