Эконометрическая модель. Классификация эконометрических моделей.

Основой механизма эконометрического моделирования является эконометрическая модель. Экономический объект в такой модели описывается и изучается с помощью эмпирических (статистических) данных. Эконометрическая модель учитывает реальные условия существования объекта и не противоречит общим законам экономики. Ошибка предсказаний по такой модели не превосходит заданной величины.

Общий вид эконометрической модели Y = f (X) + ε

Y – наблюдаемое значение зависимой переменной (объясняемая переменная, результат)

F (X) – объясненная часть, которая зависит от значение объясняющих переменных (факторов)

ε – случайная составляющая (ошибка)

Классификация эконометрических моделей

Можно выделить три основных класса моделей, которые применяются для анализа и прогнозирования экономических систем

· модели временных рядов;

· регрессионные модели с одним уравнением;

· системы одновременных уравнений.

Ø Модели временных рядов

Модели временных рядов представляют собой модели зависимости результативного признака от времени.

К ним относятся

· модели кривых роста (трендовые модели),

· адаптивные моде­ли,

· модели авторегрессии и скользящего среднего.

Примеры моделей:

1. Модели, описывающие зависимость от времени:

- тренда

- сезонности

- тренда сезонности

2. Модели, представляющие зависимость результата от переменных,

Датированных другими моментами времени:

- с распределенным лагом

С помощью таких моделей можно решать задачи прогнозирования объема продаж, спроса на продукцию, краткосрочного прогноза процентных ставок и др.

Ø Регрессионные модели с одним уравнением

В регрессионных моделях зависимая (объясняемая) переменная Y может быть представлена в виде функции f (X₁, X₂, X₃, … X_k), где - независимые (объясняющие) переменные, или факторы; k – количество факторов. В качестве зависимой переменной может выступать практически любой показатель, харак­теризующий, например, деятельность предприятия или курс ценной бумаги.

Результативный признак представлен в виде функции от факторных признаков

Y = f (X1, X2, … X_k ) + 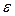объясняющая составляющая

f (X1, X2, … X_k) = Mz(Y)(ожидаемое значение результатаYпри заданных значениях факторовX1, X2, … X_k )

Уравнение регрессионной модели имеет вид Y = Mz(Y) +

В зависимости от вида функции f ( ) модели делятся на линейные и нелинейные. В зависимости от количества включенных в модель факторов Х модели делятся на однофакторные (парная модель регрессии) и многофакторные (модель множественной регрессии).

Примеры моделей:

1. Модель цены поставки.

2. Модель спроса от цены на отдельный товар от реальных доходов потребителей.

3. Модель зависимости объема производства от производственных факторов

Ø Системы одновременных уравнений

Сложные соци­ально-экономические явления иногда невозможно адекватно описать с помощью только одного соотношения (уравнения). Модели с одним уравнением не отражают взаимосвязей между объясняющими переменными или их связей с другими переменными. Кроме того, некоторые перемен­ные могут оказывать взаимные воздействия и трудно од­нозначно определить, какая из них является зависимой, а какая независимой переменной. Поэтому при построении эконометрической модели прибегают к системам уравнений.

Системы одновременных уравнений состоят из тождеств и регрессионных уравнений, в которых наряду с факторными признаками включены результативные признаки из других уравнений системы. В системе уравнений одни и те же переменные одновременно рассматриваются как зависимые переменные в одних уравнениях и независимые - в других. В тождествах вид и значения параметров известны, в уравнениях параметры оценивают.

Примеры моделей:

1. Модель спроса и предложения

2. Кейнсианская модель формирования доходов

Эконометрическое моделирование представляет собой комплексное решение целого ряда задач, поэтому весь процесс разделен на этапы. Такое разделение условно, однако позволяет понять сущность действий в эконометрическом моделировании.