Алгоритм проверки статистической гипотезы. (25)

Порядок действий для проверки статистической гипотезы:

Шаг 1.

формулируется основная статистическая гипотеза (описательный этап, формализованная запись)

Шаг 2.

создается случайная переменная z, связанная с выдвинутой гипотезой и с известным законом распределения (t), т.к. у случайной переменной, которая содержится в сформулированной основной гипотезе закон распределения может быть неизвестен (т.е. ничего нельзя сказать о ее поведении). Как правило, используются две переменные: дробь Стьюдента и дробь Фишера.

Шаг 3.

создается значение доверительной вероятности

Доверит. вероятность – область определения, созданная случайной переменной z. Данная область разбивается на две пересекаемые подобласти:

1) где гипотеза принимается z( )

2) где гипотеза 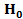отклоняется (не принимается), а принимается 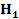: z( )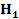

Разбиение области определения осуществляется так, чтобы оказалось справедливые следующее равенство:

P(z( ) ) = -это означает, что вероятность попадания случайной переменной z в область z( 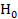) , при условии z( 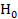) – истина, равна принятой доверительной вероятности (т.е. в области определения переменной z выделяется участок, внутри которого случайное событие окажется практически достоверным, при условии, что гипотеза - истина.

Граница, разделяющая область определения случайной переменной z – критическое значение распределения ( )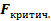

Шаг 4.

проверяется появление случайного события z, принадлежащего z( )

а) если событие появилось, то гипотеза принимается как непротиворечащая опытным (т.е. статистическим данным);

Гипотеза принимается в качестве истины с доверительной вероятностью (0,95)

–уровень значимости;

б) если событие не появилось, то гипотеза отклоняется.

Случайную переменную z называют статистикой критерия гипотезы