Корреляционный анализ в слабых шкалах
При наличии соотношения между вариацией качественных признаков говорят об их ассоциации, взаимосвязанности. Для оценки тесноты связи в этом случае используют ряд показателей.
Коэффициент ассоциации и контингенции.Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации и контингенции. Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, то есть состоящим из двух качественно отличных друг от друга значений признака (например, изделие годное или бракованное).
Таблица 1.1
Вычисление коэффициентов ассоциации и контингенции
| a | b | a+b |
| c | d | c+d |
| a+c | b+d | a+b+c+d |
В этой таблице a, b, c, d являются частотами. Коэффициенты вычисляются по формулам: 
, 
. Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если 
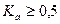или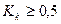 
.
Пример.Исследуем связь между успеваемостью студентов и обеспеченностью учебно-методической литературой по курсу «Эконометрика». Результаты обследования характеризуются следующими данными:
| Успеваемость | Численность студентов, чел. | Из них | |
| обеспечены учебно-методической литературой | не обеспечены учебно-методической литературой | ||
| Успевают | |||
| Не успевают | |||
| Итого |
Тогда 
.
Таким образом, связь между успеваемостью студентов и обеспеченностью учебно-методической литературой по курсу «Эконометрика» имеет место.
Задание. С помощью коэффициентов взаимной сопряженности (ассоциации и контингенции) определите связь между смертностью населения различных расовых групп и местом их рождения. Умерло человек в год в одной из европейских стран:
| Раса | Место рождения | Всего | |
| Европа | Африка | ||
| Негроидная | |||
| Европеоидная | |||
| Итого |
Ранговые коэффициенты связи. В анализе социально-экономических явлений часто приходится прибегать к различным условным оценкам с помощью рангов, а взаимосвязь между отдельными признаками измерять с помощью непараметрических коэффициентов связи.
Ранжирование –это процедура упорядочивания объектов изучения, которая выполняется на основе предпочтения.
Ранг - порядковый номер значений признака, расположенных в порядке возрастания или убывания величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех значений принимается равным средней арифметической из соответствующих номеров мест, которые они занимают. Данные ранги называются связными.
Среди непараметрических методов оценки тесноты связи наибольшее значение имеют ранговые коэффициенты Спирмена и Кендалла. Эти коэффициенты могут быть использованы для определения тесноты связи как между количественными, так и между качественными признаками. Коэффициент корреляции Спирмена рассчитывается по формул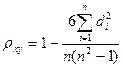е: 
, где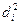 
- квадраты разности рангов, а 
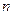- число наблюдений. Данный коэффициент принимает любые значения в интервале [-1; 1]. При проверки значимости коэффициента корреляции Спирмена исходят из того, что в случае справедливости нулевой гипотезы об отсутствии корреляционной связи между переменными статистика 
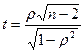имеет 
- распределение Стьюдента с 
степенями свободы. Коэффициент ранговой корреляции Спирмена значим на уровне 
, если 
, где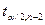 
- табличное значение критерия Стьюдента, определенное на уровне значимости при числе степеней свободы . Критическое значение - статистики рассчитывается с помощью функции MS Excel СТЬЮДРАСПОБР, в панели которой вводятся значения пороговой значимости (например, 0,05) и степени свободы 
, где 
- количество независимых переменных.
Пример. По данным об объеме строительно-монтажных работ, выполненных собственными силами, и численности работающих в 10 строительных компаниях одного из городов РФ, определить зависимость между этими признаками с помощью коэффициента Спирмена. Расчет коэффициента Спирмена и исходные данные представлены ниже.
| № строительной компании | Объем работ, тыс.руб. | Численность работающих, чел. | Ранги | Разность рангов |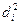
| |
| 
| |||||
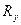
| -8 | ||||||
| -5 | ||||||
| Итого |
Тогда 
. Проверим на значимость коэффициент корреляции Спирмена. Значение критерия Стьюдента равно 
. Табличное значение на уровне значимости 0,05 и степени свободы 8 равно 
=1,86. Нулевая гипотеза принимается, корреляционная связь между признаками отсутствует.
Коэффициент корреляции Кендаллатакже может использоваться для измерения взаимосвязи между качественными и количественными признаками, характеризующими однородные объекты и ранжированные по одному принципу. Расчет рангового коэффициента Кендалла осуществляется по формуле: 
, где 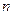- число наблюдений, S – сумма разностей между числом последовательностей и числом инверсий по второму признаку. Расчет данного коэффициента выполняется в следующей последовательности:
1. Значения признака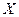 
ранжируются в порядке возрастания или убывания.
2. Значения признака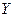 
располагаются в порядке, соответствующем значениям .
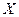3. Для каждого ранга 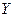определяется число следующих за ним значений рангов, превышающих его величину. Суммируя таким образом числа определяется величина 
, как мера соответствия последовательностей рангов по 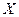и 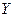и учитывается со знаком (+).
4. Для каждого ранга 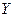определяется число следующих за ним значений рангов, меньших его величины. Суммарная величина обозначается через 
и фиксируется со знаком (-).
5. Определяется сумма баллов по всем членам ряда.
В приведенном выше примере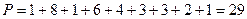 
, 
. Таким образом,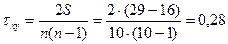 
, что свидетельствует о практическом отсутствии связи между рассматриваемыми признаками по данной совокупности компаний.
Ранговые коэффициенты Спирмена и Кендалла имеют то преимущество, что с помощью их можно измерять и оценивать связи как между количественными, так и между атрибутными признаками, которые поддаются ранжированию.
Задания для самостоятельного решения:
1.Экспертами оценивались вкусовые качества разных вин. Суммарные оценки получены следующие:
| Марка вина | Оценка, баллы | Цена, усл .ед. |
| 1,57 | ||
| 1,60 | ||
| 2,00 | ||
| 2,10 | ||
| 1,70 | ||
| 1,85 | ||
| 1,80 | ||
| 1,15 | ||
| 2,30 | ||
| 2,40 |
Согласуется ли оценка вина с его ценой? Проверьте это методами ранговой корреляции.
2. По ряду районов края определены: среднесуточное количество йода в воде и пище и пораженность населения заболеванием щитовидной железы.
| Номер района | Количество йода в воде и пище, усл. ед. | Пораженность населения заболеванием щитовидной железы, % |
| 0,2 | ||
| 0,6 | ||
| 1,1 | ||
| 0,8 | ||
| 2,5 | ||
| 4,4 | ||
| 16,9 |
Для оценки тесноты связи пораженности заболеванием щитовидной железы с количеством йода в воде и пище определите коэффициенты корреляции рангов Спирмена и Кендалла.
3. С помощью методов периодизации выделены периоды однотипной динамики безработицы и преступности.
| Год | Лица в трудоспособном возрасте, не занятые в экономике, тыс. чел. | Число зарегистрированных преступлений |
| 117,1 | ||
| 134,7 | ||
| 191,9 | ||
| 215,0 |
По рассматриваемому периоду с помощью линейного коэффициента корреляции определите наличие связи между числом преступлений и численностью лиц, не занятых в экономике.
4. Исследовалась социально-демографическая характеристика случайных потребителей наркотиков от их семейного положения в одном из регионов РФ в 2003 году.
| Потребление наркотиков | Общее число потребителей, тыс. чел. | Из них в разрезе семейного положения | |
| Замужем (женат) | Не замужем (не женат) | ||
| Потреблял | 24,5 | 10,0 | 14,5 |
| Не потреблял | 7,0 | 2,5 | 4,5 |
| Итого | 31,5 | 12,5 | 19,0 |
Рассчитайте коэффициенты ассоциации и контингенции. Сформулируйте выводы, вытекающие из анализа полученных коэффициентов.
5. Зависимость между объемом промышленной продукции и инвестициями в основной капитал по 10 областям одного из федеральных округов РФ в 2003 году характеризуется следующими данными:
| Область | Объем промышленной продукции, млрд руб. | Инвестиции в основной капитал, млрд руб. |
| Белгородская | 64,6 | 10,22 |
| Брянская | 21,5 | 4,12 |
| Владимирская | 51,1 | 8,58 |
| Воронежская | 54,4 | 14,79 |
| Ивановская | 20,6 | 2,88 |
| Калужская | 35,7 | 7,24 |
| Костромская | 18,4 | 5,57 |
| Курская | 37,1 | 9,67 |
| Липецкая | 90,6 | 10,45 |
| Смоленская | 39,8 | 10,48 |
Вычислите ранговые коэффициенты корреляции Спирмена и Кендалла. Сформулируйте вывод о зависимости между объемом промышленной продукции и инвестициями в основной капитал по рассматриваемым областям РФ.