Взаимосвязь случайных переменных. Ковариация и коэффициент корреляции пары случайных величин и их оценивание.

Под случайной величиной понимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно – заранее не известно).

Ковариация служит для характеристики тесноты связи между случайными величинами. Если (x,y) — пара случайных переменных, то их ковариацией называется константа С_ху=Cov(x,y)=E(x·y)-E(x)·E(y)

Свойства математического ожидания позволяют представить С_ху и так: С_ху=E((x-m_x)·(y-m_y)), где m_x=E(x), m_y=E(y)

Для вычисления С_ху нужно знать закон распределения P_xy(q, r) пары (x,y). Если он неизвестен, то ковариацию можно оценить по выборке из генеральной совокупности Ω(x,y): {(x₁, y₁), (x₂, y₂),…,(x_n, y_n)}

Оценкой ковариации служит величина

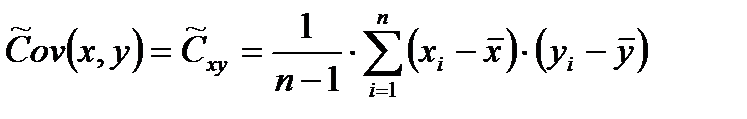
именуемая выборочной ковариацией.

Также тесноту связи определяют при помощи коэффициента корреляции. Существует разные модификации формула данного показателя:

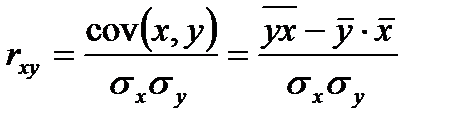, причем -1≤r_xy≤1

Если |r_xy|=1, то y=a₀+a₁x. Так что при |r_xy|=1 между переменными (x,y) существует жесткая (функциональная) линейная связь.