Оценка параметров множественной регрессии методом наименьших квадратов

Как и в случае парной регрессии, целью метода является выбор вектора оценок b, минимизирующего сумму квадратов остатков e_i (т. е. квадрат длины вектора остатков e):

.

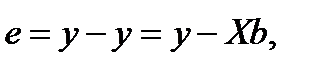
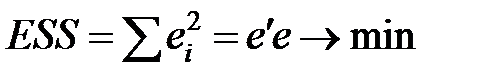Выразим ee' через Х и b:

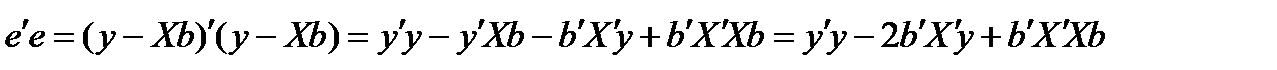
Необходимые условия минимума ESS получаются дифференцированием по вектору :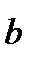

,

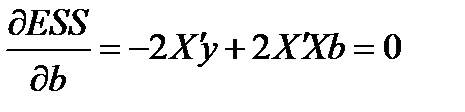откуда, учитывая обратимость матрицы Х'Х, находим оценку метода наименьших квадратов

.

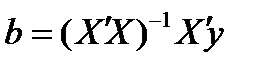Получим полезную в дальнейшем формулу для суммы квадратов остатков:

.

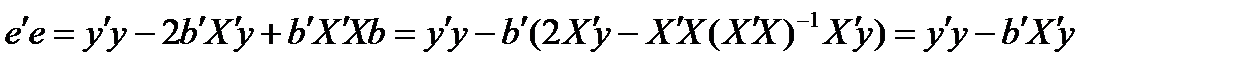Можно доказать (теорема Гаусса – Маркова), что оценка метода наименьших квадратов (10.1) является эффективной (в смысле наименьшей дисперсии) оценкой в классе линейных несмещенных оценок