Регрессии нелинейные по оцениваемым параметрам.

Различают два класса нелинейных регрессий:

· регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам;

· регрессии, нелинейные по оцениваемым параметрам.

К нелинейным регрессиям по оцениваемым параметрам относятся функции:

· показательная – у = аb^х ε;

· экспоненциальная –

· степенная –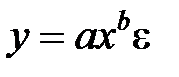

Данный класс нелинейных моделей подразделяется на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные. Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Если нелинейная модель внутренне нелинейна,то она не может быть сведена к линейной функции.

Например, в эконометрических исследованиях при изучении эластичности спроса от цен широко используется степенная функция:

y=ax^bε,

где у – спрашиваемое количество; х – цена; ε – случайная ошибка.

Данная модель нелинейна относительно оцениваемых пaраметров, ибо включает параметры а и b. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию еприводит его к линейному виду:

lnу = lnа + b lnx + lnε.

Если же модель представить в виде y=ax^b + εто она становится внутренне нелинейной, ибо ее невозможно превратить в линейный вид.