Выбор формы уравнения регрессии

Как и в парной зависимости, возможны разные виды уравне­ний множественной регрессии: линейные и нелинейные.

Ввиду четкой интерпретации параметров наиболее широко используются линейная и степенная функции. В линейной мно­жественной регрессии

парамет­ры при х называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

В степенной функции 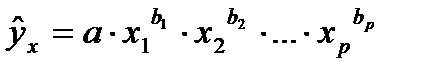коэффициенты являются коэффициентами эластичности. Они показывают, на сколько процентов изменяется в среднем результат с изменением соответствующего фактора на 1 % при неизменности действия других факторов. Этот вид уравнения регрессии получил наибольшее распространение в производственных функциях, в исследованиях спроса и потребления.

В производственных функциях вида

где Р – количество продукта, изготавливаемого с помощью m производственных факторов (F₁, F₂, …,F_m);

b - параметр, являющийся эластичностью количеств продукции по отношению к количеству соответствующих производственных факторов.

Экономический смысл имеет не только коэффициенты b каждого фактора, но их сумма, т.е. сумма эластичностей: .

Эта величина фиксирует обобщенную характеристику эластичности производства.

Вопросы для самоконтроля

1. Как образуется множественная регрессия?

2. Цель множественной регрессии?

3. Экономический смысл коэффициента b?

 

Рекомендуемая литература

1. Кристофер Доугерти. Введение в эконометрию. – М.: ИНФРА – М, 2001 - 402 с.

2. С.А. Бородич. Эконометрика. Минск ООО «Новое знание» 2001.

3. Р.У. Рахметова Краткий курс по эконометрике. Учебное пособие. Алматы. 2004. -78с.

4. И.И. Елисеева .Эконометрика. – М.: «Финансы и статистика»,2002

5. Ежемесячный информационно-аналитический журнал.

Тема №7. Предпосылки метода наименьших квадратов.

 

· Метод наименьших квадратов

Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов (МНК). При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки параметров регрессии.

Так, для уравнения 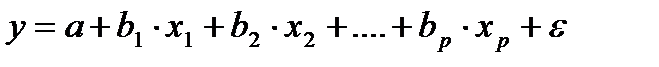система нормальных уравнений составит

Ее решение может быть осуществлено методом определителей:

где - определитель системы;

а, b₁, …, b_p - частные определители.

При этом

где - получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.

Другой вид уравнения множественной регрессии – уравнение регрессии в стандартизованном масштабе:

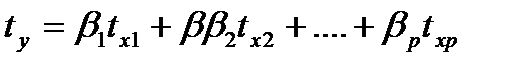
где - стандартизованные переменные;

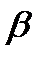- стандартизованные коэффициенты регрессии.

Вопросы для самоконтроля

1. Какой метод используется при определение параметров регрессии?

2. Цель множественной регрессии?

3. Экономический смысл коэффициента b?

 

Рекомендуемая литература

1. Кристофер Доугерти. Введение в эконометрию. – М.: ИНФРА – М, 2001 - 402 с.

2. С.А. Бородич. Эконометрика. Минск ООО «Новое знание» 2001.

3. Р.У. Рахметова Краткий курс по эконометрике. Учебное пособие. Алматы. 2004. -78с.

Тема №8. Оценка параметров и надежности результатов уравнения множественной регрессии.

 

· Оценка параметров и надежности результатов уравнения множественной регрессии

 

Оценка статистическая значимости параметров регрессии проводится с помощью t – статистики Стьюдента и путем расчета доверительного интервала для каждого из показателей. Выдвигается гипотеза Н₀ о статистически значимом отличие показателей от 0 a = b = r = 0. Рассчитываются стандартные ошибки параметров a,b, r и фактическое значение t – критерия Стьюдента.

; ; ;

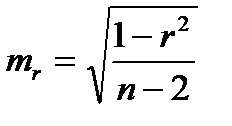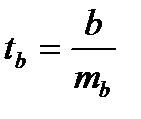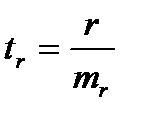
Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-критерия Фишера:

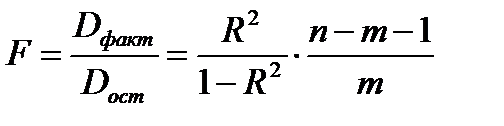
где 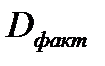- факторная сумма квадратов на одну степень свободы;

- остаточная сумма квадратов на одну степень свободы;

- коэффициент (индекс) множественной детерминации;

m - число параметров при переменных х (в линейной регрессии совпадает с числом включенных в модель факторов);

n - число наблюдений.

Оценивается значимость не только уравнения в целом, но и фактора, дополнительно включенного в регрессионную модель. Необходимость такой оценки связана с тем, что не каждый фактор, вошедший в модель, может существенно увеличивать долю объясненной вариации результативного признака. Кроме того, при наличии в модели нескольких факторов они могут вводиться в модель в разной последовательности.

Ввиду корреляции между факторами значимость одного и того же фактора м/б различной в зависимости от последовательности его введения в модель. Мерой для оценки включения фактора в модель служит частый F-критерий, т.е. F_xi. В общем виде для фактора x_i частый F-критерий определяется как :

Если рас­сматривается уравнение y=a+b₁x₁+b₂+b₃x₃+e, то определяются последовательно F-критерий для уравнения с од­ним фактором х₁, далее F-критерий для дополнительного включе­ния в модель фактора х₂, т. е. для перехода от однофакторного уравнения регрессии к двухфакторному, и, наконец, F-критерий для дополнительного включения в модель фактора х₃, т. е. дается оценка значимости фактора х₃ после включения в модель факто­ров x₁ и х₂. В этом случае F-критерий для дополнительного вклю­чения фактора х₂ после х₁ является последовательнымв отличие от F-критерия для дополнительного включения в модель фактора х₃, который является частнымF-критерием, ибо оценивает значи­мость фактора в предположении, что он включен в модель по­следним. С t-критерием Стьюдента связан именно частный F-критерий. Последовательный F-критерий может интересовать исследователя на стадии формирования модели. Для уравнения y=a+b₁x₁+b₂+b₃x₃+e оценка значимости коэффициентов регрессии b_i предпола­гает расчет трех межфакторных коэффициентов детерминации, а именно: 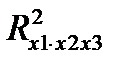, , 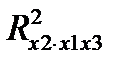и можно убедиться, что существует связьмежду собой t- критерия Стьюдента для оценки значимости b_i и частным F-критерием:

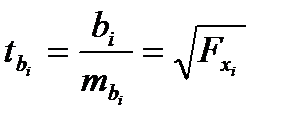На основе соотношения b_i и получим:

Продемонстрируем это соотношение на примере двухфакторного уравнения регрессии 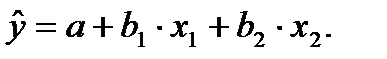Ранее было доказано, что коэффициенты регрессии 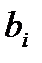могут быть определены как

Тогда для двухфакторного уравнения регрессии имеем:

Тогда связь с скорректированным коэффициентом множественной корреляции или детерминацией :

 

Величина F-критерия, оценивая значимость уравнения регрессии в целом, характеризует одновременно и значимость коэффициента (индекса) множественной корреляции. Вместе с тем оценку существенности коэффициента множественной корреляции можно дать и через сравнение скорректированного коэффициента корреляции с его табличным значением при соответствующем уровне вероятности и числе степеней свободы n-m-1. Так, при n = 30 и m = 2 фактическое значение должно превышать 0,368 при 5%-ном уровне значимости, чтобы можно было считать его значение отличным от нуля с вероятностью 0,95.

 

Вопросы для самоконтроля

1. Какой метод используется при определение?

2. Цель множественной регрессии?

3. Экономический смысл коэффициента b?

 

Рекомендуемая литература

1. Кристофер Доугерти. Введение в эконометрию. – М.: ИНФРА – М, 2001 - 402 с.

2. С.А. Бородич. Эконометрика. Минск ООО «Новое знание» 2001.

3. Р.У. Рахметова Краткий курс по эконометрике. Учебное пособие. Алматы. 2004. -78с.

4. И.И. Елисеева .Эконометрика. – М.: «Финансы и статистика», 2002.

5. Ежемесячный информационно-аналитический журнал.

Тема №9. Множественная корреляция. Линейный коэффициент множественной корреляции. Частная корреляция.

 

· Множественная корреляция

· Частная корреляция

 

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации.

Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или, иначе, оценивает тесноту совместного влияния факторов на результат.

Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:

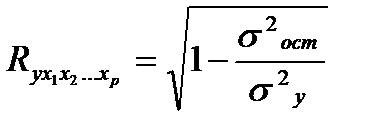
где - остаточная дисперсия для уравнения

-общая дисперсия результативного признака.

Расчет индекса множественной корреляции предполагает определение уравнения множественной регрессии и на его основе остаточной дисперсии:

При линейной зависимости признаков формула индекса множественной корреляции имеет вид:

где -стандартизованные коэффициенты регрессии;

Формула индекса множественной корреляции для линейной регрессии получила название линейного коэффициента множественной корреляции, или, что то же самое, совокупного коэффициента корреляции.

Индекс детерминации для нелинейных по оцениваемым параметрам функции в некоторых работах по эконометрике принято называть «квази -R²»

При нелинейной зависимости формула скорректированного индекса множественной детерминации имеет вид:

Чем больше величина m, тем сильнее различия и .

Для линейной зависимости признаков скорректированный коэффициент множественной корреляции определяется по той же формуле, что и индекс множественной корреляции, т.е. как корень квадратный из . Отличие состоит лишь в том, что в линейной зависимости под m подразумевается число факторов, включенных в регрессионную модель, а в криволинейной зависимости m - число параметров при х и их преобразованиях (х², lnx и др.), которое может быть больше числа факторов как экономических переменных.

Частные коэффициенты (или индексы) корреляции характери­зуют тесноту связи между результатом и соответствующим фак­тором при устранении влияния других факторов, включенных в уравнение регрессии.

Показатели частной корреляции представляют собой отно­шение сокращения остаточной дисперсии за счет дополнитель­ного включения в анализ нового фактора к остаточной диспер­сии, имевшей место до введения его в модель.

Частные коэффициенты корреляции измеряющие влияние на у фактора х_i при неизменном уровне других факторов можно определить по формуле:

;

При двух факторах и i=1 данная формула примет вид:

Частные коэффициенты корреляции изменяются в пределах от -1 до 1, а по формуле через множественные коэффициенты детерминации – о 0 до 1. Сравнение их друг с другом позволяет ранжировать факторы по тесноте их связи с результатом.

 

 

Вопросы для самоконтроля

1. Какая практическая значимость уравнения множественной регрессии?

2. Что характеризует коэффициент множественной корреляции?

 

 

Рекомендуемая литература

1. Кристофер Доугерти. Введение в эконометрию. – М.: ИНФРА – М, 2001 - 402 с.

2. С.А. Бородич. Эконометрика. Минск ООО «Новое знание» 2001.

3. Р.У. Рахметова Краткий курс по эконометрике. Учебное пособие. Алматы. 2004. -78с.

4. И.И. Елисеева .Эконометрика. – М.: «Финансы и статистика»,2002

5. Ежемесячный информационно-аналитический журнал.

Тема №10. Отбор факторов. Мультиколлинеарность.

 

· Отбор факторов

· Мультиколлинеарность

 

Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требова­ниям.

1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий ко­личественного измерения, то ему нужно придать количествен­ную определенность

2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.

Включение в модель факторов с высокой интеркорреляцией, когда R_yx1 < R_x1x2 для зависимости 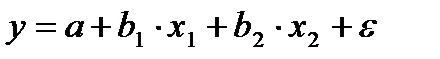может привести к нежелательным последствиям — система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.

Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.

Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором р факторов, то для нее рассчитывается показа­тель детерминации R, который фиксирует долю объясненной ва­риации результативного признака за счет рассматриваемых в регрессии р факторов. Влияние других не учтенных в модели факторов оценивается как 1-R² с соответствующей остаточной дисперсией S².

При дополнительном включении в регрессию р + 1 фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться:

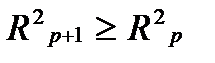и

Если же этого не происходит и данные показатели практически мало отличаются друг от друга, то включаемый в анализ фактор х_р+1 не улучшает модель и практически является лишним фактором.

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.

Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы были бы равны нулю. Так, для уравнения, включающего три объясняющих переменных

матрица коэффициентов корреляции между факторами имела бы определитель, равный единице:

.

Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны единице, то определитель такой матрицы равен нулю:

.

Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

Существует ряд подходов преодоления сильной межфакторной корреляции. Самый простой путь устранения мультиколлинеарности состоит в исключении из модели одного или нескольких факторов. Другой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними.

Одним из путей учета внутренней корреляции факторов является переход к совмещенным уравнениям регрессии, т.е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие. Так, если , то возможно построение следующего совмещенного уравнения:

.

Рассматриваемое уравнение включает взаимодействие первого порядка (взаимодействие двух факторов). Возможно включение в модель и взаимодействий более высокого порядка, если будет доказана их статистическая значимость по -критерию Фишера, но, как правило, взаимодействия третьего и более высоких порядков оказываются статистически незначимыми.

Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости от того, какая методика построения уравнения регрессии принята, меняется алгоритм ее решения на ЭВМ.

Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:

1. Метод исключения – отсев факторов из полного его набора.

2. Метод включения – дополнительное введение фактора.

3. Шаговый регрессионный анализ – исключение ранее введенного фактора.

При отборе факторов также рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6–7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной дисперсии очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а -критерий меньше табличного значения.

 

Вопросы для самоконтроля

1. Для чего определяется мультиколлинеарность?

2. Отбор факторов как определяется?

 

 

Рекомендуемая литература

1. Кристофер Доугерти. Введение в эконометрию. – М.: ИНФРА – М, 2001 - 402 с.

2. С.А. Бородич. Эконометрика. Минск ООО «Новое знание» 2001.

3. Р.У. Рахметова Краткий курс по эконометрике. Учебное пособие. Алматы. 2004. -78с.

4. И.И. Елисеева .Эконометрика. – М.: «Финансы и статистика»,2002

5. Ежемесячный информационно-аналитический журнал.

Тема №11. Проверка выполнимости предпосылок МНК. Пошаговая регрессия.

 

· Проверка выполнимости предпосылок МНК

· Пошаговая регрессия

 

При оценке параметров уравнения регрессии применяется метод наименьших квадратов (МНК). При этом делаются определенные предпосылки относительно случайной составляющей . В модели

случайная составляющая представляет собой ненаблюдаемую величину. После того как произведена оценка параметров модели, рассчитывая разности фактических и теоретических значений результативного признака , можно определить оценки случайной составляющей . Поскольку они не являются реальными случайными остатками, их можно считать некоторой выборочной реализацией неизвестного остатка заданного уравнения, т.е. .

При изменении спецификации модели, добавлении в нее новых наблюдений выборочные оценки остатков могут меняться. Поэтому в задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений , т.е. остаточных величин.

При использовании критериев Фишера и Стьюдента делаются предположения относительно поведения остатков – остатки представляют собой независимые случайные величины и их среднее значение равно 0; они имеют одинаковую (постоянную) дисперсию и подчиняются нормальному распределению.

Статистические проверки параметров регрессии, показателей корреляции основаны на непроверяемых предпосылках распределения случайной составляющей . Они носят лишь предварительный характер. После построения уравнения регрессии проводится проверка наличия у оценок (случайных остатков) тех свойств, которые предполагались. Связано это с тем, что оценки параметров регрессии должны отвечать определенным критериям. Они должны быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют чрезвычайно важное практическое значение в использовании результатов регрессии и корреляции.

Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Если оценки обладают свойством несмещенности, то их можно сравнивать по разным исследованиям.

Оценки считаются эффективными, если они характеризуются наименьшей дисперсией. В практических исследованиях это означает возможность перехода от точечного оценивания к интервальному.

Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки. Большой практический интерес представляют те результаты регрессии, для которых доверительный интервал ожидаемого значения параметра регрессии имеет предел значений вероятности, равный единице. Иными словами, вероятность получения оценки на заданном расстоянии от истинного значения параметра близка к единице.

Указанные критерии оценок (несмещенность, состоятельность и эффективность) обязательно учитываются при разных способах оценивания. Метод наименьших квадратов строит оценки регрессии на основе минимизации суммы квадратов остатков. Поэтому очень важно исследовать поведение остаточных величин регрессии . Условия, необходимые для получения несмещенных, состоятельных и эффективных оценок, представляют собой предпосылки МНК, соблюдение которых желательно для получения достоверных результатов регрессии.

Исследования остатков предполагают проверку наличия следующих пяти предпосылок МНК:

1) случайный характер остатков;

2) нулевая средняя величина остатков, не зависящая от ;

3) гомоскедастичность – дисперсия каждого отклонения , одинакова для всех значений x;

4) отсутствие автокорреляции остатков – значения остатков распределены независимо друг от друга;

5) остатки подчиняются нормальному распределению.

Если распределение случайных остатков не соответствует некоторым предпосылкам МНК, то следует корректировать модель.

Вторая предпосылка МНК относительно нулевой средней величины остатков означает, что . Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных.

Предпосылка о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью F- и t-критериев. Вместе с тем, оценки регрессии, найденные с применением МНК, обладают хорошими свойствами даже при отсутствии нормального распределения остатков, т.е. при нарушении пятой предпосылки МНК.