Задание 13. Использовать функцию ЛИНЕЙН для задачи 2.

Функцию ЛИНЕЙН можно построить и для множественной модели. Сделать это для задачи 2 (стр.30), действуя аналогично тому, как это было сделано в предыдущем задании, только при выполнении пункта 1 следует выделить блок ячеек, состоящий из 5 строк и 3 столбцов. Результаты занести в таблицу:

Задание 14. Рассчитать оценку параметра 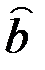для модели без константы и выполнить задания 10-12 для этой модели. Сделать выводы.

Вычислить оценку параметра 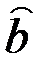для уравнения без константы по формуле

Затем составить другую расчетную таблицу. Для этого скопировать столбцы x_i, y_i, x_i², y_i², x_iy_i и вставить их в свободные ячейки. Добавить столбцы для вычисления значений , , , 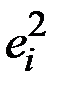и . Сделать расчеты, аналогично тому, как это было сделано при выполнении заданий 6 и 10, с той лишь разницей, что здесь . Записать результаты:

ESS = _________________ ; RSS = ______________ ;

TSS = _________________ ; ESS + RSS = ______________;

; .

Сделать выводы: _____________________________________

_________________________________________________________

Задание 15. Проверить значимость оценок параметров регресси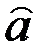и и 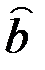при уровне значимости 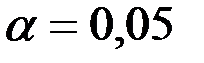. Сделать выводы и записать экономический смысл параметров регрессии.

В задании 5 была найдена оценка параметра .

Для проверки значимости этой оценки надо проверить гипотезу

H₀: ( 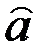не значим).

H₁: 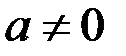( 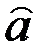значим).

Критическая область – ______________________.

Гипотеза H₀ проверяется с помощью критерия .

Подставляя в эту формулу найденные ранее значения 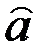и , найти

Критическую точку 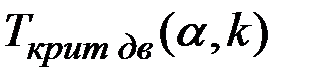, где 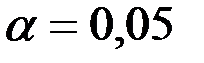, , найти с помощью функции СТЬЮДРАСПОБР аналогично тому, как это сделано в задании 3: .

Далее сравнить и и сделать вывод:

_________________________________________________________

Замечание. Даже если оценка константы уравнения регрессии 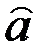оказалась незначимой, то ее все равно оставляют в модели, так как модель с константой всегда лучше, чем модель без константы.

Записать экономический смысл оценки параметра :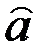

_________________________________________________________

Замечание. Оценка константы 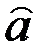уравнения регрессии не всегда допускает экономическую интерпретацию. Она имеет экономический смысл только тогда, когда факторные признаки могут принимать нулевые значения.

Аналогично проверим гипотезу о значимости оценки параметра , найденной в задании 5. Выдвигаем гипотезу

H₀: _____________________________________________

H₁: _____________________________________________

Критическая область – ______________________.

Гипотеза H₀ проверяется с помощью критерия .Подставляя в эту формулу найденные ранее значения 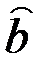и , найдем

Далее сравнить и и сделать вывод:

_________________________________________________________

Записать экономический смысл оценки параметра :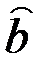

_________________________________________________________

Задание 16. Задав уровень достоверности , построить интервальные оценки для параметров a и b и сделать выводы.

Используя формулу

и учитывая, что при уровне достоверности (95%) 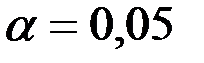, построить интервальную оценку параметра a:

___________ < a < ____________

Принимая во внимание экономическую интерпретацию параметра а, сделать вывод: ____________________________________

_________________________________________________________

Аналогично, используя формулу

Построить интервальную оценку для параметра b:

___________ < b < ____________

и сделать вывод:___________________________________________

_________________________________________________________

Замечание. Интервальные оценки параметров можно использовать для проверки значимости соответствующего параметра. Если интервальная оценка параметра содержит ноль, то параметр не значим, в противном случае параметр значим.

Задание 17. Проверить значимость модели в целом с помощью F-теста, сделать вывод и записать экономический смысл коэффициента детерминации.

В задании 4 найдено значение R²= ____________.

Для проверки гипотезы о значимости R², а следовательно, о значимости модели в целом выдвигают нулевую гипотезу:

H₀: __________________________________________________

__________________________________________________

H₁: __________________________________________________

__________________________________________________

Критическая область – ______________________

Найти наблюдаемое значение критерия

;

Затем найти с помощью функции FРАСПОБР критическую точку , учитывая, что 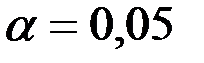, , 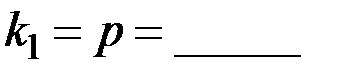. Функция FРАСПОБР используется аналогично функции СТЬЮДРАСПОБР, только надо ввести в соответствующие рабочие поля не одну, а две степени свободы.

Далее сравнить и и сделать вывод:

_________________________________________________________

Экономический смысл коэффициента детерминации:

_________________________________________________________

Задание 18. Проверить эквивалентность критериев, то есть сравнить 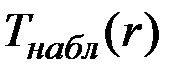, , 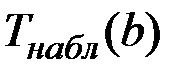и . Сделать вывод.

Найти и сравнить значения:

; ; .

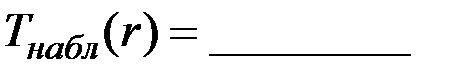Вывод: __________________________________________________

_________________________________________________________

_________________________________________________________________

_________________________________________________________

__________________________________________________________

Задание 19. Проверить существенность отличия b от .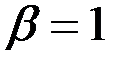

Для проверки существенности отличия b от 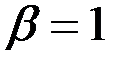следует проверить гипотезу:

H₀: _____________________________________________

H₁: _____________________________________________

Критическая область – ______________________.

Гипотеза H₀ проверяется с помощью критерия .

Подставляя в эту формулу 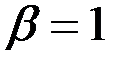и найденные ранее значения 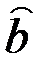и , найти значение . Сравнить его модуль с найденным выше сделать вывод:

_________________________________________________________

__________________________________________________________________

__________________________________________________________

Замечание 1. Можно проверить существенность отличия b от 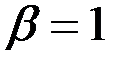с помощью интервальной оценки этого параметра: если 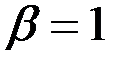принадлежит полученному интервалу, то это отличие несущественное, а если не принадлежит, то отличие значимое.

Замечание 2. Гипотеза такого вида проверяется только в случае практической необходимости, когда есть основания предполагать, что параметр b равен некоторому числу β.