Выборочная дисперсия.
Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения , вводят сводную характеристику- выборочную дисперсию.
 Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .
Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .
Если все значения признака выборки различны, то

если же все значения имеют частоты n1, n2,…,nk, то

Для характеристики рассеивания значений признака выборки вокруг своего среднего значения пользуются сводной характеристикой - средним квадратическим отклонением.
 Выборочным средним квадратическим отклоненим называют квадратный корень из выборочной дисперсии:
Выборочным средним квадратическим отклоненим называют квадратный корень из выборочной дисперсии:

Вычисление дисперсии- выборочной или генеральной, можно упростить, используя формулу:
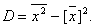
Замечание: если выборка представлена интервальным вариационным рядом, то за xi принимают середины частичных интервалов.
7. Выборочная ковариация  величин
величин  и
и 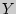 определяется формулой
определяется формулой

где  , а
, а  ,
,  - выборочные средние величин
- выборочные средние величин  и
и 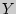 . При небольшом количестве экспериментальных данных
. При небольшом количестве экспериментальных данных  удобно находить как полный вес ковариационного графа:
удобно находить как полный вес ковариационного графа:
-

- Если
 — независимые случайные величины, то:
— независимые случайные величины, то:

- Но обратное утверждение, вообще говоря, неверно: из отсутствия ковариации не следует независимость. Пример:
Пусть случайная величина  принимает значения
принимает значения  , каждое с вероятностью
, каждое с вероятностью  . Тогда
. Тогда  будет принимать значения −1, 0 и 1, каждое с вероятностью
будет принимать значения −1, 0 и 1, каждое с вероятностью  , а
, а  . Тогда
. Тогда  , но
, но 
- Ковариация случайной величины с собой равна дисперсии:
 .
. - Ковариация симметрична:
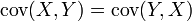 .
.
- В силу линейности математического ожидания, ковариация может быть записана как
 .
.
- Пусть
 случайные величины, а
случайные величины, а  их две произвольные линейные комбинации. Тогда
их две произвольные линейные комбинации. Тогда
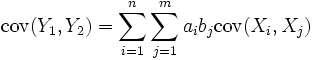 .
.
В частности ковариация (в отличие от коэффициента корреляции) не инвариантна относительно смены масштаба, что не всегда удобно в приложениях.
- Если
 и
и  — числа, то
— числа, то
 .
.
- Неравенство Коши-Буняковского: если принять в качестве скалярного произведения двух случайных величин ковариацию
 , то квадрат нормы случайной величины будет равен дисперсии
, то квадрат нормы случайной величины будет равен дисперсии  , и Неравенство Коши-Буняковского запишется в виде:
, и Неравенство Коши-Буняковского запишется в виде:
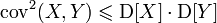 .
.
- ковариация(Y;X) = коэффициент корреляции (Х;Y)* ско(X)*СКО(Y)[1]
Если ковариация положительна, то с ростом значений одной случайной величины, значения второй имеют тенденцию возрастать, а если знак отрицательный — то убывать.
Однако только по абсолютному значению ковариации нельзя судить о том, насколько сильно величины взаимосвязаны, так как её масштаб зависит от их дисперсий. Масштаб можно отнормировать, поделив значение ковариации на произведение стандартных отклонений (квадратных корней из дисперсий). При этом получается так называемый коэффициент корреляции Пирсона, который всегда находится в интервале от −1 до 1.
Случайные величины, имеющие нулевую ковариацию, называются некоррелированными. Независимые случайные величины всегда некоррелированы, но не наоборот.
8. Выборочный коэффициент корреляциинаходится по формуле

где  - выборочные средние квадратические отклонения величин
- выборочные средние квадратические отклонения величин  и
и 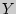 .
.
Выборочный коэффициент корреляции  показывает тесноту линейной связи между
показывает тесноту линейной связи между  и
и 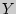 : чем ближе
: чем ближе  к единице, тем сильнее линейная связь между
к единице, тем сильнее линейная связь между  и
и 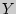 .
.
Корреляционной зависимостью 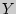 от
от  называют функциональную зависимость условной средней
называют функциональную зависимость условной средней 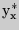 от
от  .
.
 представляет уравнение регрессии
представляет уравнение регрессии 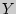 на
на  , а
, а  - уравнение регрессии
- уравнение регрессии  на
на 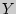 .
.
Корреляционная зависимость может быть линейной и криволинейной. В случае линейной корреляционной зависимости выборочное уравнение прямой линии регрессии 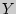 на
на  имеет вид:
имеет вид:

Параметры 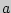 и
и  уравнения прямой
уравнения прямой  линии регрессии
линии регрессии 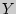 на
на  можно находить по методу наименьших квадратов из системы уравнений
можно находить по методу наименьших квадратов из системы уравнений

9. Точечные оценки параметров распределения.
Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Возникает задача оценки параметров, которыми определяется это распределение.
Обычно в распоряжении исследователя имеются лишь данные выборки, полученные в результате n наблюдений (здесь и далее наблюдения предполагаются независимыми). Через эти данные и выражают оцениваемый параметр. Рассматривая значения количественного признака как независимые случайные величины, можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения - это значит найти функцию от наблюдаемых случайных величин, которая и дает приближенное значение оцениваемого параметра.
 Итак, статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.
Итак, статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.
Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям: оценка должна быть несмещенной, эффективной и состоятельной.
Поясним каждое из понятий.
 Несмещенной называют статистическую оценку Q*, математическое ожидание которой равно оцениваемому параметру Q при любом объеме выборки, т. е.
Несмещенной называют статистическую оценку Q*, математическое ожидание которой равно оцениваемому параметру Q при любом объеме выборки, т. е.
M(Q*) = Q.
 Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.
Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.
 Эффективной называют статистическую оценку, которая (при заданном объеме выборки п) имеет наименьшую возможную дисперсию.
Эффективной называют статистическую оценку, которая (при заданном объеме выборки п) имеет наименьшую возможную дисперсию.
При рассмотрении выборок большого объема (n велико!) к статистическим оценкам предъявляется требование состоятельности.
 Состоятельной называют статистическую оценку, которая при п®¥ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при п®¥ стремится к нулю, то такая оценка оказывается и состоятельной.
Состоятельной называют статистическую оценку, которая при п®¥ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при п®¥ стремится к нулю, то такая оценка оказывается и состоятельной.
 Рассмотрим точечные оценки параметров распределения, т.е.
Рассмотрим точечные оценки параметров распределения, т.е.
оценки, которые определяются одним числом Q* =f( x1, x2,…,xn), где x1, x2,…,xn- выборка.
10. Интервальные оценки параметров распределения.
 Интервальной называют оценку, которая определяется двумя числами—концами интервала. Интервальные оценки позволяют установить точность и надежность оценок .
Интервальной называют оценку, которая определяется двумя числами—концами интервала. Интервальные оценки позволяют установить точность и надежность оценок .
Пусть найденная по данным выборки статистическая характеристика Q* служит оценкой неизвестного параметра Q. Будем считать Q постоянным числом (Q может быть и случайной величиной). Ясно, что Q* тем точнее определяет параметр Q, чем меньше абсолютная величина разности |Q- Q*|. Другими словами, если d>0 и |Q- Q*| <d , то чем меньше d , тем оценка точнее.
 Таким образом, положительное число d характеризует точность оценки.
Таким образом, положительное число d характеризует точность оценки.
Однако статистические методы не позволяют категорически утверждать, что оценка Q* удовлетворяет неравенству |Q- Q*| <d; можно лишь говорить о вероятности g, с которой это неравенство осуществляется.
 Надежностью (доверительной вероятностью) оценки называют вероятность g , с которой осуществляется неравенство |Q—Q* | <d .
Надежностью (доверительной вероятностью) оценки называют вероятность g , с которой осуществляется неравенство |Q—Q* | <d .
Обычно надежность оценки задается наперед, причем в качестве g берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.
Пусть вероятность того, что, |Q- Q*| <d равна g:
P(|Q- Q*| <d)= g.
Заменив неравенство равносильным ему двойным неравенством получим:
Р [Q* —d< Q < Q* +d] = g
Это соотношение следует понимать так: вероятность того, что интервал Q* - d< Q < Q* +d заключает в себе (покрывает) неизвестный параметр Q, равна g.
Интервал (Q* - d Q* +d) называется доверительным интервалом , который покрывает Доверительный интервал для оценки математического ожидания при известном s.
Пусть количественный признак генеральной совокупности распределен нормально. Известно среднее квадратическое отклонение этого распределения -s. Требуется оценить математическое ожидание а по выборочной средней. Найдем доверительный интервал, покрывающий а с надежностью g. Выборочную среднюю будем рассматривать как случайную величину ( она изменяется от выборки к выборке), выборочные значения признака- как одинаково распределенные независимые СВ с математическим ожиданием каждой а и средним квадратическим отклонением s. Примем без доказательства, что если величина Х распределена нормально, то и выборочная средняя тоже распределена нормально с параметрами
 .
.
Потребуем, чтобы выполнялось равенство
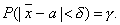
Заменив Х и s, получим
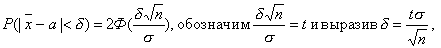
получим

Задача решена. Число t находят по таблице функции Лапласа Ф(х).
Пример1. СВХ распределена нормально и s =3. Найти доверительный интервал для оценки математического ожидания по выборочным средним, если n = 36 и задана надежность g =0,95.
Из соотношения 2Ф(t)= 0,95 , откуда Ф(t) = 0,475 по таблице найдем t : t =1,96. Точность оценки

 неизвестный параметр с надежностью g.
неизвестный параметр с надежностью g.
Т.к. мы не знакомы с законами распределения СВ, которые используются при выводе формулы, то примем ее без доказательства.
В качестве неизвестного параметра s используют исправленную дисперсию s2 . Заменяя s на s, t на величину tg. Значение этой величины зависит от надежности g и объема выборки n и определяется по " Таблице значений tg." Итак :

и доверительный интервал имеет вид

Требуется оценить неизвестную генеральную дисперсию и генеральное среднее квадратическое отклонение по исправленной дисперсии, т.е. найти доверительные интервалы, покрывающие параметры D и s с заданной надежностью g.
Потребуем выполнения соотношения
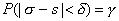 .
.
Раскроем модуль и получим двойное неравенство:
 .
.
Преобразуем:
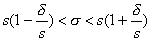 .
.
Обозначим d/s = q (величина q находится по "Таблице значений q"и зависит от надежности и объема выборки), оверительный интервал для оценки генерального среднего квадратического отклонения имеет вид:
 .
.
Замечание : Так как s >0, то если q >1 , левая граница интервала равна 0:
0< s < s ( 1 + q ).