Векторная оптимизация
К общей формулировке многокритериальной задачи могут сводиться задачи различного содержания, которые можно подразделить на четыре типа.
1. Задачи оптимизации на множестве целей, каждая из которых должна быть учтена при выборе оптимального решения. Примером может служить задача составления плана работы предприятия, в которой критериями служит ряд экономических показателей.
2. Задачи оптимизации на множестве объектов, качество функционирования каждого из которых оценивается самостоятельным критерием. Если качество функционирования каждого объекта оценивается несколькими критериями (векторным критерием), то такая задача называется многовекторной. Примером может служить задача распределения дефицитного ресурса между несколькими предприятиями. Для каждого предприятия критерием оптимальности является степень удовлетворения его потребности в ресурсе или другой показатель, например, величина прибыли. Для планирующего органа критерием выступает вектор локальных критериев предприятий.
3. Задачи оптимизации на множестве условий функционирования. Задан спектр условий, в которых предстоит работать объекту, и применительно к каждому условию качество функционирования оценивается некоторым частным критерием.
4. Задачи оптимизации на множестве этапов функционирования. Рассматривается функционирование объектов на некотором интервале времени, разбитом на несколько этапов. Качество управления на каждом этапе оценивается частным критерием, а на множестве этапов - общим векторным критерием.
Многокритериальные задачи можно также классифицировать по другим признакам: по вариантам оптимизации, по числу критериев, по типам критериев, по соотношениям между критериями, по уровню структуризации, наличию фактора неопределенности.
При разработке методов решения векторных задач приходится решать ряд специфических проблем.
Проблема нормализации возникает в связи с тем, что локальные критерии имеют, как правило, различные единицы и масштабы измерения, и это делает невозможным их непосредственное сравнение. Операция приведения критериев к единому масштабу и безразмерному виду носит название нормирования. Наиболее распространенными способами нормирования является замена абсолютных значений критериев их безразмерными относительными величинами
или относительными значениями отклонений от оптимальных значений критериев
Проблема выбора принципа оптимальности связана с определением свойств оптимального решения и решением вопроса — в каком смысле оптимальное решение превосходит все остальные.
Проблема учета приоритета критериев встает, если локальные критерии имеют различную значимость. Необходимо найти математическое определение приоритета и степень его влияния на решение задачи.
Проблема вычисления оптимума возникает, если традиционные вычислительные схемы и алгоритмы непригодны для решения задачи векторной оптимизации.
Решение перечисленных проблем идет в нескольких направлениям. Основные направления:
методы, основанные на свертывании критериев в единый;
методы, использующие ограничения на критерии;
методы целевого программирования;
методы, основанные на отыскании компромиссного решения;
методы, в основе которых лежат человеко-машинные процедуры принятия решений (интерактивное программирование).
В методах, основанных на свертывании критериев, из локальных критериев формируется один. Наиболее распространенным является метод линейной комбинации частных критериев. Пусть задан вектор весовых коэффициентов критериев а = {al,...,ak}, характеризующих важность соответствующего критерия, 
Линейная скаляризованная функция представляет собой сумму частных критериев, умноженных на весовые коэффициенты. Задача математического программирования становится однокритериальной и имеет вид
Критерии в свертке могут быть нормированы. Решение, полученное в результате оптимизации скаляризованного критерия эффективно.
К недостаткам метода можно отнести то, что малым приращениям коэффициентов соответствуют большие приращения функции, т. е. решение задачи неустойчиво, а также необходимость определения весовых коэффициентов.
Направление методов, использующих ограничения на критерии включает два подхода:
1) метод ведущего критерия;
2) методы последовательного применения критериев (метод последовательных уступок, метод ограничений).
Метод ведущего критерия
В методе ведущего критерия все целевые функции кроме одной переводятся в разряд ограничений. Пусть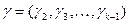 
- вектор, компоненты которого представляют собой нижние границы соответствующих критериев. Задача будет иметь вид
Полученное этим методом решение может не быть эффективным, поэтому необходимо проверить его принадлежность области компромиссов.
Метод ведущего критерия применяется в таких задачах, как минимизация полных затрат при условии выполнения плана по производству различных видов продукции, максимизация выпуска комплектных наборов при ограничении на потребляемые ресурсы.
Метод последовательных уступок
Алгоритм метода последовательных уступок:
1. Критерии нумеруются в порядке убывания важности.
2. Определяется значение 
. Лицом, принимающим решение, устанавливается величина уступки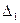 
по этому критерию.
3. Решается задача по критерию 
с дополнительным ограничением 
Далее пункты 2 и 3 повторяются для критерия, ... , 
.
Пример.Решить задачу
методом последовательных уступок, если уступка по первому критерию составляет 10% от его оптимального значения.
Решение. Решим задачу по критерию 
.Получим 
= 160. В соответствии с условием задачи величина уступки 
. Дополнительное ограничение будет иметь вид 
, то есть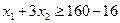 
. Решая задачу
получим 
.
Метод равных и наименьших отклонений
При решении задач линейного программирования методом уступок мы имеем различные отклонения критериев от экстремальных значений. Потребуем, чтобы в компромиссном плане относительные отклонения всех критериев от своих экстремальных значений были равны и минимальны. При этом предполагается, что в области допустимых решений задачи не существует плана, оптимизирующего все критерии.
Условие равенства отклонений запишем в виде
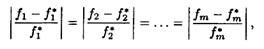
где — экстремальное значение целевой функции 
Если некоторым критериям отдается предпочтение, то в условие равенства отклонений вводятся соответствующие коэффициенты 
(коэффициент 
считается равным единице). В этом случае соотношение примет вид
Предполагая, например, что все критерии задачи максимизируются, условие равенства отклонений после соответствующих преобразований запишем в виде
или
где 
m — число критериев задачи.
Для случая, когда один критерий максимизируется, а второй минимизируется, условие равенства отклонений запишется так:
Поскольку относительные отклонения для всех критериев равны, для минимизации достаточно взять любое из отклонений. Возьмем, например, отклонение первого критерия
Чтобы его уменьшить, надо увеличить, приближая к максимальному значению . Новая задача, которая называется замещающей, решается на максимум переменной . Аналогично решается замещающая задача и по второму критерию.
Для критерия, который минимизируется, например, для третьего, относительное отклонение
будет минимальным, когда 
окажется приближенным к своему наименьшему значению 
, т.е. будет найден минимум функции .
В качестве целевой функции можно взять любое из следующих выражений:
Тогда все остальные требования выполняются автоматически.
Итак, чтобы решить задачу линейного программирования методом равных и наименьших относительных отклонений, необходимо составить так называемую замещающую задачу, т. е. к системе ограничений данной задачи добавить дополнительные условия
где оптимизируемые критерии 
включены в число неизвестных.
Проиллюстрируем метод равных и наименьших относительных отклонений на примере.
Пример.Решить задачу линейного программирования по двум критериям:
Решение. Решаем задачу по первому критерию. Максимальное значение целевой функции
(max) = 14.
Решаем по второму критерию. Минимальное значение целевой функции 
(min) = 3.
Поскольку в задаче производится максимизация и минимизация, дополнительным условием равных относительных отклонений будет
где
Дополнительное условие равных относительных отклонений после подстановки значений 
и примет вид
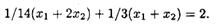
Упрощая данное соотношение, получаем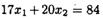
или
Составляем ограничения замещающей задачи:
В качестве целевой функции взят первый критерий задачи, который максимизируется. Аналогично можно было бы взять в качестве целевой функции и второй критерий. Тогда задача решалась бы на минимум второго критерия.
После решения замещающей задачи получаем, следующий план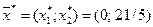 
, для которого 