Намагничивающая сила трехфазной обмотки.

 

Намагничивающая сила обмотки является базой для определения потока.

Запишем намагничивающие силы для трех фаз в виде пульсирующих волн, а затем разложим их на прямую и обратную волну, затем их сложим, то получим намагничивающую силу трехфазной обмотки

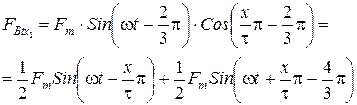
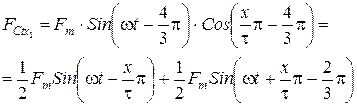
сложив прямые волны получим.

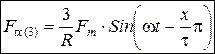+0,

сумма обратных волн равна 0, т.к. сдвиг на 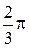и

Намагничивающая сила трехфазной обмотки есть сумма прямых волн, что это бегущая волна, которая двигается вдоль зазора с синхронной скоростью и с постоянной амплитудой. Эта н.с. создает вращающееся магнитное поле, которое движется вдоль зазора с синхронной скоростью и постоянной амплитудой.

Покажем графически, что три пульсирующие волны трех фаз создают в любой момент времени бегущую волну с постоянной амплитудой, рис. 103.

Рис. 103

Для изменения направления движения волны необходимо поменять чередование фаз, т.е. сменить любые две фазы.

 

Намагничивающие силы высших гармоник

 

Вопрос о высших гармонических намагничивающих сил очень сложен. Высшие гармоники могут быть пространственные и временные. Мы рассматриваем пространственные высшие гармоники, вызванные расположением самой обмотки в пространстве.

Амплитуда намагничивающей силы n гармоники запишется

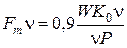
Высшие гармоники намагничивающих сил однофазной обмотки

Пульсирующая волна.

,

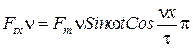разложим на две бегущие волны

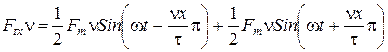
Здесь тоже будет прямая и обратная волна.

Скорость прямой волны

, ; ;

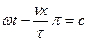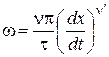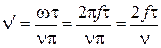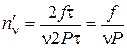
Скорость обратной волны

т.е. скорость н.с. n гармоники в n раз меньше основной гармоники.

 

Высшие гармоники намагничивающих сил трехфазной обмотки

 

Если намагничивающие силы высших гармоник трех фаз разложить на прямую и обратную волну, а затем их сложить, то будет видно, что высшие гармоники н.с. будут вести себя по-разному.

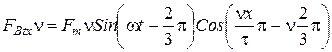
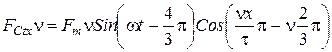
1. Гармоники четные исчезнут, т.к. гармоники симметричны оси абсцисс.

2. Гармоники кратные 3-м выпадут. n = 3, т.к. 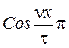- для всех трех фаз будет иметь cos одного и того же угла, а сумма же амплитуд сдвинутых на угол 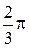и с одинаковыми амплитудами равна нулю.

Другие гармоники будут вести себя по разному, одни будут вращаться в одну сторону, другие в другую при одном чередовании фаз.

Гармоники порядка , где а = 1, 2, 3. n = 5, 11, 17 … которым соответствует выражение

Эти гармоники будут вращаться в обратную сторону по отношению к н.с. первой гармоники, рис. 104.

Посмотрим чередование фаз.

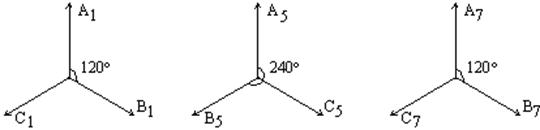
Для первой гармоники A1 - B1 = 120°

A5–B5=120×5=600=360 + 240° обратное чередование фаз

A7–В7=120×7=840=2×360+120° прямое чередование фаз

Рис. 104

Гармоники порядка 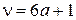, n = 7, 13, 19 будут вращаться в сторону первой гармоники.