Структура систем эконометрических уравнений

Объектом статистического изучения в экономике являются сложные системы. При использовании отдельных уравнений регрессии изменение факторов влечет за собой, как правило, изменения во всей системе взаимосвязанных признаков. Именно поэтому в последние десятилетия в экономических, биометрических и социологических исследованиях важное место заняла проблема описания структуры связей между переменными системой одновременных уравнений. Различают несколько видов систем уравнений, применяемых в эконометрике:

– система независимых уравнений – когда каждая зависимая переменная y рассматривается как функция одного и того же набора факторов х_i

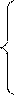y₁= a₁₁x₁+ a₁₂x₂+…+ a_1mx_m+ε₁,

y₂= a₂₁x₁+ a₂₂x₂+…+ a_2mx_m+ε₂,

………………………………………

y_n= a_n1x₁+ a_n2x₂+…+ a_nmx_m+ε_n.

Для построения такой системы и нахождения ее параметров используется метод наименьших квадратов, применяемый к каждому уравнению в отдельности;

– система рекурсивных уравнений – когда зависимая переменная у одного уравнения выступает в виде фактора х в другом уравнении

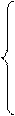y₁= a₁₁x₁+ a₁₂x₂+…+ a_1mx_m+ε₁,

y₂=b₂₁y₁ + a₂₁x₁+ a₂₂x₂+…+ a_2mx_m+ε₂,

y₃=b₃₁y₁ + b₃₂y₂ + a₃₁x₁+ a₃₂x₂+…+ a_3mx_m+ε₃,

………………………………………………………

y_n=b_n1y₁ + b_n2y₂ +…+ b_nn-1y_n-1+ a_n1x₁+ a_n2x₂+…+ a_nmx_m+ε_n.

Для построения такой системы и нахождения ее параметров используется метод наименьших квадратов, применяемый последовательно к каждому уравнению в отдельности, начиная с первого;

– система взаимосвязанных (совместных) уравнений – когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую

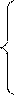y₁=b₁₂y₂ + b₁₃y₃ +…+ b_1ny_n+ a₁₁x₁+ a₁₂x₂+…+ a_1mx_m+ε₁,

y₂=b₂₁y₁ + b₂₃y₃ +…+ b_2ny_n+ a₂₁x₁+ a₂₂x₂+…+ a_2mx_m+ε₂,

…………………………………………………………………..

y_n=b_n1y₁ + b_n2y₂ +…+ b_nn-1y_n-1+ a_n1x₁+ a_n2x₂+…+ a_nmx_m+ε_n.

Такая система уравнений называется структурной формой модели. Для построения таких систем и нахождения их параметров используются косвенный и двухшаговый методы наименьших квадратов.

Зависимые переменные (у), число которых равно числу уравнений в системе, называются эндогенными переменными, предопределенные переменные (х), влияющие на эндогенные переменные, но не зависящие от них, называются экзогенными переменными.

Экономические переменные могут выступать в одних моделях как эндогенные, а в других как экзогенные переменные. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно получать целевые значения эндогенных переменных.

Примером системы одновременных уравнений может служить модель динамики цены и заработной платы вида

y₁=b₁₂y₂ + a₁₁x₁+ ε₁,

y₂=b₂₁y₁ + a₂₂x₂+ a₂₃x₃+ε₂,

где y₁– темп изменения месячной заработной платы;

y₂ – темп изменения цен;

х₁ – процент безработных;

х₂ – темп изменения постоянного капитала;

х₃ – темп изменения цен на импорт сырья.

Система линейных функций эндогенных переменных от всех предопределенных переменных системы называется приведенной формой модели

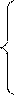y₁= δ₁₁x₁+ δ₁₂x₂+…+ δ_1mx_m+ε₁,

y₂= δ₂₁x₁+ δ₂₂x₂+…+ δ_2mx_m+ε₂,

………………………………………

y_n= δ_n1x₁+ δ_n2x₂+…+ δ_nmx_m+ε_n.

 

где δ_ij – коэффициенты приведенной формы модели.