Примеры
1. Оценить линейную регрессию, построить график, найти коэффициент корреляции, стандартные ошибки коэффициентов регрессии, дать интерпретацию уравнению регрессии и коэффициентов корреляции.
А)
| x | 1351.7 | 1369.3 | 1479.1 | 1682.5 | 1799.0 | 1924.5 | 2046.0 |
| y | 117,9 | 122,5 | 125,5 | 129,2 | 134,3 | 138,4 | 141,0 |
Здесь х – совокупные личные доходы;
y – текущие расходы на одежду среднестатистической американской семьи с 1996 по 2002 г.
Оценим регрессию y=ax+b.
Рассчитайте коэффициенты a и b по формулам (2.5).
Ответ:
y=78,967+0.031x
Найдем коэффициент корреляции по формуле (2.2):
rxy=0.986
Построим график:
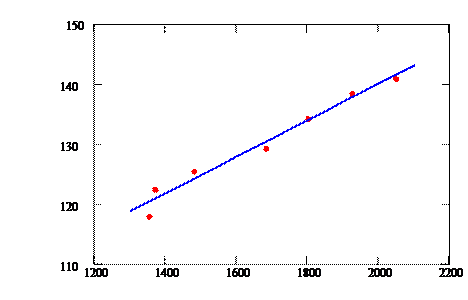
Вывод: С каждого дополнительного доллара американская семья в период 1996-2002 г. тратила 3,1 центов на текущие расходы на одежду.
Б)
| x | 1351.7 | 1369.3 | 1479.1 | 1682.5 | 1799.0 | 1924.5 | 2046.0 |
| y | 164,3 | 173,7 | 181,3 | 243,2 | 337,9 | 376,4 | 356,6 |
Здесь х – совокупные личные доходы;
y – текущие расходы на бензин, среднестатистической американской семьи с 1996 по 2002 г.
Оценим регрессию y=ax+b.
Рассчитайте коэффициенты a и b по формулам (2.5).
Ответ:
y= -281,825+0.327x
Найдем коэффициент корреляции по формуле (2.2):
rxy=0.962
Построим график:
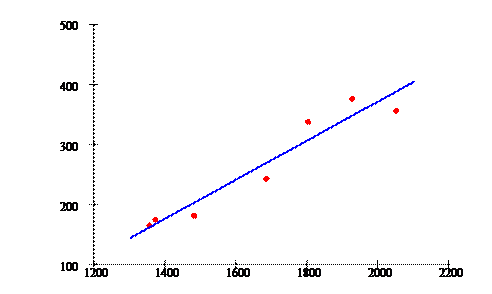
Вывод: С каждого дополнительного доллара американская семья в период 1996-2002 г. тратила 32,7 центов на текущие расходы на бензин.
2. Вычислить коэффициенты регрессии общей суммы налогового сбора (переменная y) на сумму поступлений налога на добавленную стоимость (х) данным:
| Время наблюдения | y, млрд. руб. | x, млрд. руб. | xi2 | yi2 | xiyi |
| январь | 38,9 | 13,4 | 179,56 | 1513,21 | 521,26 |
| февраль | 45,3 | 15,4 | 237,16 | 2052,09 | 697,62 |
| март | 61,1 | 16,7 | 278,89 | 3733,21 | 1020,37 |
| апрель | 70,4 | 16,2 | 262,44 | 4956,16 | 1140,48 |
| май | 63,8 | 13,0 | 4070,44 | 829,4 | |
| июнь | 67,7 | 15,0 | 4583,29 | 1015,5 | |
| июль | 70,6 | 20,8 | 432,64 | 4984,36 | 1468,48 |
| август | 78,9 | 16,4 | 268,96 | 6225,21 | 1293,96 |
| сентябрь | 73,2 | 17,4 | 302,76 | 5358,24 | 1273,68 |
| октябрь | 78,1 | 23,6 | 556,96 | 6099,61 | 1843,16 |
| ноябрь | 103,0 | 23,9 | 571,21 | 2461,7 | |
| декабрь | 133,4 | 34,4 | 1183,36 | 17795,56 | 4588,96 |
| Σ | 884,4 | 226,1 | 4667,94 | 71980,4 | 18154,6 |
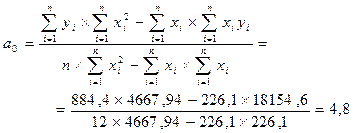
График уравнения регрессии y на x выглядит следующим образом:
 |
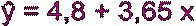3. у= b +ах b и а - ?
| № | Х | Y | X2 | XY |
| -3 | -0,71 | 2,13 | ||
| -2 | -0,1 | 0,02 | ||
| -1 | 0,51 | -0,51 | ||
| 0,82 | ||||
| 0,88 | 0,88 | |||
| 0,81 | 1,62 | |||
| 0,49 | 1,47 | |||
| Сум å | 2,79 | 5,61 |
Оценим регрессию y=ax+b.
Рассчитайте коэффициенты a и b по формулам (2.5).
Ответ:
y= 0,40+0,20x – уравнение линейной регрессии
4. х – мощность пласта, у – смена добычи угля.
| № | Х | Y | X2 | XY |
| Сум å |
a = 10*664-94*68 = 1.02
10*908-(94)2
b = 68-(-2,75)*94 = –2.75
10
Уравнение регрессии
y= 1,02x–2,75.
Коэфф. корреляции
R= n*åxy–åxåy = 10*664 –94*68 =0.866
Ö(n*åx2– (x)2)(n*åy2– (åy)2) Ö(10*908– (94)2)(10*496– (68)2)
Связь между Х и Y ближе к линейной.
Коэфф. детерминации R2 ½R½£1
Þ 0.8662 = 0.749 Þ на 74,9% смена добычи угля зависит от мощности пласта и 25,1% от других факторов.
Контрольные вопросы
1. Что понимается под парной регрессией?
2. Какие задачи решаются при построении уравнения регрессии?
3. Какой вид имеет система нормальных уравнений метода наименьших квадратов в случае линейной регрессии?
4. По какой формуле вычисляется линейный коэффициент парной корреляции?
5. Как строится доверительный интервал для линейного коэффициента парной корреляции?
6. Как вычисляется индекс корреляции?
7. Как вычисляется и что показывает индекс детерминации?
8. Как проверяется значимость уравнения регрессии и отдельных коэффициентов?
9. Как строится доверительный интервал прогноза в случае линейной регрессии?
10. В чем сущность метода наименьших квадратов (МНК)?
11. Сформулируйте общую задачу статистической оценки параметров на примере оценки параметров линейной регрессии.
12. Сформулируйте свойства несмещенности, состоятельности и эффективности оценок параметров. Обладают ли этими свойствами оценки параметров линейной регрессии, полученные с помощью МНК?
13. В чем различие, смысловое и количественное, теоретических значений коэффициентов регрессии и их выборочных значений?
14. Какие факторы влияют на величину стандартных ошибок выборочных коэффициентов регрессии?
15. Как связаны выборочные коэффициенты регрессии с коэффициентом корреляции величин х и у?
16. Как осуществляется прогнозирование экономических показателей с использованием моделей линейной регрессии?
17. Как можно оценить «естественный» уровень безработицы с использованием модели линейной регрессии?
18. В каких случаях необходимо уточнение линейной регрессионной модели и как оно осуществляется?