Измерение и интерпретация случайной составляющей.

Надежность получаемых оценок a₀ и a₁ зависит от дисперсии отклонений переменной у от оцененной линии регрессии e_i = у_i – aх_i - b_. Несмещенная оценка дисперсии случайной составляющей вычисляется по формуле

, (2.7)

и является мерой разброса зависимой переменной вокруг линии регрессии (необъясненная дисперсия).

В качестве меры того, насколько хорошо регрессия описывает данную систему наблюдений, служит коэффициент детерминации, при этом вычисляются следующие суммы квадратов отклонений:

S²=å_i(y_i– 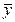)² – фактических значений от их среднего арифметического;

Ŝ²= å_i (ŷ_i – 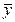)² – выровненных значений от среднего арифметического

фактических значений;

Š²= å_i (y_i – ŷ _i)² – фактических от выровненных значений.

Имеет место равенство S²= Ŝ² + Š².

Коэффициент детерминации есть отношение объясненной части вариации ко всей вариации в целом

R²=Ŝ²/S²=1 – Š²/S². (2.8)

Таким образом, чем «ближе» этот коэффициент к единице, тем лучше описание, разумеется, если при этом модель методически правильна.

В столбцах 8 и 10 табл.2.1 вычислены выровненные значения эмпирической функции регрессии и квадраты их отклонений от наблюденных значений.

В соответствии с (2.7) получаем оценку дисперсии случайной составляющей

=0,0479/6=0,008.

В соответствии с (2.8) значение коэффициента детерминации

R²= 1 – Š²/S² = 1 – 0,0479/1,66=0,971

показывает, что 97,1% общей вариабельности розничного товарооборота объясняется изменениями числа работников, в то время как на все остальные факторы приходится лишь 2,9% вариабельности.

Найденные отклонения фактических значений от выровненных (столбец 9) позволяют провести сравнительный анализ работы различных магазинов. Прежде всего, необходимо обратить внимание на магазины с отрицательным отклонением (3, 4, 6). Особенно велико отклонение у 4-го магазина. Необходимо внимательно обследовать эти магазины и установить причины отклонений. Это может быть расположение магазина в стороне от основных потоков покупателей, плохое обслуживание, неудовлетворительный кадровый состав и т.п. Здесь, по-видимому, имеются резервы в организации труда работников. Напротив, в магазинах 1, 2, 5, 7 и 8 работники используются эффективнее статистического «норматива», но может оказаться, что эти магазины объективно находятся в лучших условиях.

Обозначим S_x=å_i(x_i – )², тогда дисперсия параметра a₁ вычисляется по формуле D(a₁)=σ²/ S_x.

Значимость оцененного коэффициента регрессии a₁ может быть проверена с помощью анализа его отношения к своему стандартному отклонению

t=a₁/ÖD(a₁). (2.9)

Эта величина имеет распределение Стьюдента с (n – 2) степенями свободы и называется t-статистика. (см. приложение 1). Можно использовать следующее грубое правило для оценки значимости коэффициента линейной регрессии:

- если t<1, то он не может быть признан значимым, поскольку доверительная вероятность здесь составляет менее 0,7;

- если 1<t<2, то сделанная оценка может рассматриваться как более или менее значимая, доверительная вероятность здесь примерно от 0,7 до 0,95;

- значение 2<t<3, свидетельствует о весьма значимой связи (доверительная вероятность от 0,95 до 0,99);

- t>3 есть практически стопроцентное свидетельство ее наличия.

Сформулированными правилами можно надежно пользоваться при n³10.

При большом размере выборки повторяющиеся пары наблюдений группируются в виде корреляционной таблицы. Если n_yx – количество наблюдений одинаковых пар (х,у), то для вычисления коэффициента корреляции в формуле (2.1) необходимо брать ху=ån_yxx_iy_i/n.

Для оценки тесноты любой корреляционной связи вводится корреляционное отношение Y к Х как отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению признака Y:

h_yx=s_Yx/s_y. (2.10)

Здесь s_Yx=√(Sn_x(y_x – y)²)/n,

s_y = √Sn_y(y – y)²)/n,

где n – объем выборки (сумма всех частот); n_x – частота значения х признака Х; n_y – частота значения у признака Y; y – общая средняя признака Y; y_x – условная средняя признака Y.

Чем ближе корреляционное отношение к 1, тем теснее связь между признаками, однако, оно не задает вида этой связи и не позволяет судить о степени близости наблюдений к какой-либо кривой.

Пример 2.2. Пусть имеется распределение 50 га пахотной земли по количеству внесенных удобрений х (ц на 1 га) и по урожайности у (ц с 1 га), приведенное в табл. 2.2. В этой таблице, например, число 4, стоящее на пересечении 1-й строки и 1-го столбца, показывает, что на 4 га из 50 было внесено по 10 ц удобрений и при этом получена урожайность по 15 ц с га. Найти уравнение прямой линии регрессии Y на Х, коэффициент корреляции и корреляционное отношение по данным корреляционной табл. 2.2.

Таблица 2.2

у	х
			ny
		–
nх				n =50
ух

Вычислим сначала все средние и дисперсии:

у=(38×15+12×25)/50=17.4,

х=(10×10+28×20+12×30)/50=20.4,

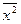=(10×100+28×400+12×900)/50=460,

ху=(4×10×15+28×20×15+6×30×15+6×10×25+6×30×25)/50=354,

s_х = Ö 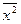– ( )² =Ö460 – 20.4² =Ö43.84=6.62,

s_y =Ö(38× (15 – 17.4)² +12× (25 – 17.4)²)/50=4.27,

s_Yx =Ö(10× (21 – 17.4)²+28× (15 – 17.4)²+12× (20 – 17.4)²)/50=Ö7.44=2.73.

Тогда коэффициент корреляции из (2.2)

r_yx =(354 – 20.4×17.4)/(6.62×4.27)= – 0.034,

коэффициент регрессии из (2.6)

r_yx = –0.034×4.27/6.62= –0.022,

уравнение прямой регрессии имеет вид

у_х – 17.4= –0.022(х – 20.4) или у_х = –0.022х + 17.85

и корреляционное отношение из (2.10)

h_yx=2.73/4.27=0.64.

Из вычисленных показателей можно сделать следующий вывод:

Линейной связи между признаками нет, но какая-то связь есть, причем весьма существенная. Диаграмма рассеяния и прямая линия регрессии построены на рис.2.1. (В кружках проставлены n_yx).

 

25

у_х = -0.022х+17.85

15

 

 

10 20 30

Рис.2.1. Диаграмма рассеяния (пример 2.2).

2.7. Практический блок