Регрессия по эмпирическим (выборочным) данным и теоретическая регрессия.
Пример 2.1. Исследуем зависимость розничного товарооборота (млрд. руб.) магазинов от среднесписочного числа работников. В табл.2.1 во втором и третьем столбцах приведены значения соответственно объемов розничного товарооборота(у) и среднесписочного числа работников(х), а в следующих столбцах – значения необходимых расчетных величин.
Таблица 2.1
| номер | у | х | (х – 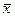 )2 )2
| (у – 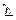 )2 )2
| х2 | ху | ŷ | ε | ε2 |
| 0,5 | 0,49 | 36,5 | 0,43 | 0,07 | 0,0049 | ||||
| 0,7 | 0,25 | 59,5 | 0,661 | 0,039 | 0,0015 | ||||
| 0,9 | 0,09 | 91,8 | 0,998 | -0,098 | 0,0096 | ||||
| 1,1 | 0,01 | 126,5 | 1,239 | -0,139 | 0,0193 | ||||
| 1,4 | 0,04 | 170,8 | 1,373 | 0,027 | 0,0007 | ||||
| 1,4 | 0,04 | 176,4 | 1,45 | -0,05 | 0,0025 | ||||
| 1,7 | 0,25 | 227,8 | 1,604 | 0,096 | 0,0092 | ||||
| 1,9 | 0,49 | 279,3 | 1,854 | 0,046 | 0,0021 | ||||
| сумма | 9,6 | 1,66 | 1168,6 | 9,592 | 0,001 | 0,0479 | |||
| средн. | 1,2 | 544,5 | 0,2075 | 13313,5 | 146,075 | 1,199 | 0,0001 | 0,0060 |
В соответствии с (2.5)
a=( 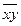 –
–  ×
× 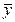 )/(
)/( 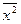 – (
– ( 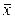 )2) =(146,075 – 113×1,2)/544,5=0,01924;
)2) =(146,075 – 113×1,2)/544,5=0,01924;
b=(( 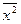 ) ×
) × 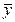 –
–  ×
× 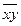 )/(
)/( 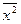 –(
–(  )2)=(13313,5×1,2–113×146,075)/544,5= -0,974.
)2)=(13313,5×1,2–113×146,075)/544,5= -0,974.
Таким образом, получено уравнение регрессии
ŷ = – 0,974 + 0,01924х.