Чистый сдвиг и его особенности

Сдвиг

Сдвиг, КРУЧЕНИЕ

Контрольные вопросы

1. Когда брус испытывает деформацию изгиба?

2. Какой изгиб называется прямым?

3. Какой изгиб называется чистым?

4. Какой изгиб называется поперечным?

5. Что такое балка?

6. Какие внутренние усилия возникают в брусе при изгибе? Как они определяются?

7. Контроль эпюр Q и М по дифференциальным зависимостям?

8. Какие напряжения возникают в балке при чистом изгибе? Как они определяются?

9. Какие напряжения возникают в балке при поперечном изгибе? Как они определяются?

10. Условие прочности балки при изгибе по нормальным напряжениям?

11. В чём заключается полная проверка прочности балки?

12. Какие перемещения возникают в поперечном сечении балки? Как они определяются?

13. Как определяется жёсткость при изгибе?

 

 

Сдвигом называется такой вид нагружения, при котором в поперечных сечениях бруса из шести внутренних усилий отличными от нуля являются только поперечные силы.

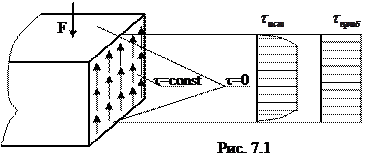Такой вид нагружения встречается редко. Чаще всего он сопровождается изгибающими мо-ментами. Однако, в некоторых случаях, например, в заклёпочных, болтовых, сварных сое-динениях имеет место нагружение близкое к сдвигу. При этом распределение касательных напряжений неравномерно. Так как внешние поверхности свободны от осевых нагрузок, топо закону парности касательных напряжений в верхних и нижних точках сечения . Из уравнения равновесия следует .Как показывают исследования, распределение 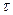по высоте сечения близко к равномерному (τ=const) , поэтому и , где А – площадь среза.

Условие прочности : 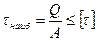, (7.1)

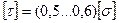- для пластических материалов и 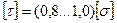- для хрупких материалов.

 

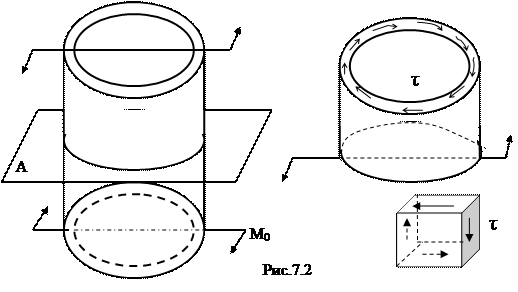Чистым сдвигом называется такой вид плоского напряженного состояния, при котором по граням элементарного параллелепипеда, выделенного в окрестности рассматриваемой точки, действуют одни лишь касательные напряжения.

Вкачестве примера такого напряженного состояния можно рассмотреть тонкостенную цилиндрическую трубку, нагруженную по торцам парами сил (рис.7.2). Рассечем её плоскостью А, отбросим верхнюю часть и покажем оставшуюся нижнюю часть. В сечении действуют касательные напряжения τ, величина которых определится из условия равенства момента равномерно распределенных по сечению внутренних сил внешнему моменту М₀: 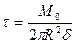, где R – средний радиус трубки, δ – её толщина.

Нормальных напряжений в этом сечении не будет. Вырежем из стенки бесконечно малый элемент в виде кубика. На его нижней грани будут действовать касательные напряжения такие же, как и на верхней, но в противоположном направлении. На передней и задней стенках напряжений нет. Так как элемент должен находиться в равновесии, то на боковых стенках также должны быть касательные напряжения, которые создают пару сил, но направленную в противоположную сторону.

При чистом сдвиге длины ребер элементарного параллелепипеда не изменяются, а изменяются углы между гранями (рис. 7.3). Верхняя грань параллелепипеда перемещается относительно противоположной грани на величину δ, называемую абсолютным сдвигом.

 

маций tgγ = γ, тогда 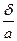= γ(рад).

Как показывает опыт, угол сдвига γ прямо пропорционален касательным напряжениям. Эта зависимость между γ и τ называется законом Гука при сдвиге и записывается выражением

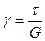, или 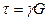. (7.2)

Коэффициент пропорциональности G называется модулем сдвига (или модулем упругости второго рода). Он как и модуль продольной упругости Е измеряется в паскалях (Па) или в мегапаскалях (МПа).