Решение.

Пример 3.

Теорема 3. (Теорема Бернулли).

Пусть проводится n независимых испытаний по схеме Бернулли, тогда при неограниченном увеличении числа испытаний частота случайного события сходится по вероятности к вероятности события, т.е.

, (3)

Если вероятность события от испытания к испытанию не меняется и равна p (q=1- p).

Монету подбрасывают 1000 раз. Оценить снизу вероятность отклонения частоты появления «герба» от вероятности его появления меньше, чем на 0,1.

Здесь n=1000, p=q=1/2, ε=0,1. Используя неравенство (3), получим:

Неравенство 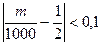равносильно двойному неравенству 400<m<600; поэтому можно сказать, что вероятность числа попаданий «герба» в интервал (400, 600) больше .

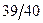Одним из наиболее замечательных результатов, установленных теорией вероятности, является утверждение о том, что закон распределения суммы большого числа случайных величин приближается к нормальному.