Лекция № 9.
Тема: примеры рекуррентных соотношений
Основные вопросы, рассматриваемые на лекции:
1. Задача о ханойской башне
2. Разрезание пиццы
3. Задача Флавия
Краткое содержание лекционного материала
1. Задача о ханойской башне. Эту головоломку придумал французский математик Э. Люк в 1883 г. Формулировка задачи «Ханойская башня»:
Есть три стержня: A, B и C. На стержень A надето 8 колец: наверху самое маленькое, каждое следующее больше предыдущего, а внизу самое большое. Два других стержня пусты. Необходимо перенести все кольца со стержня A на стержень C, чтобы на стержне C кольца были в том же порядке, в котором они исходно находились на стержне A. Брать за один ход несколько колец нельзя. Кроме того, никогда нельзя класть большее кольцо поверх меньшего.

Рекуррентное отношение для решения задачи «Ханойская башня»: пусть  – число ходов для решения задачи, где
– число ходов для решения задачи, где 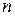 – число колец; тогда представим, что верхние
– число колец; тогда представим, что верхние  колец перенесены на стержень
колец перенесены на стержень  (за
(за  ходов); тогда за один ход нижнее кольцо перенесем на стержень
ходов); тогда за один ход нижнее кольцо перенесем на стержень  ; затем за
; затем за  ходов верхние
ходов верхние  колец на стержень
колец на стержень  ; получим
; получим  . Значит,
. Значит,  .
.
Алгоритм: нечетный шаг – нужно перемещать верхнее кольцо, четный шаг – произведем единственно возможное перемещение оставшихся колец. Если перенумеровать кольца по порядку, то четные и нечетные кольца будут перемещаться в различных направлениях по кругу.
2. Разрезание пиццы. Впервые эта задача была решена в 1826 г. швейцарским математиком Я. Штейнером. Формулировка задачи: на какое максимальное число  областей можно разделить плоскость
областей можно разделить плоскость 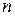 прямыми?
прямыми?

Рассмотрев случаи  можно подумать, что
можно подумать, что  . Однако уже при
. Однако уже при  получается
получается  . Рекуррентное соотношение:
. Рекуррентное соотношение:  .
.
Решение:  .
.
3. Задача Флавия основана на легенде, что отряд Флавия не пожелал сдаваться в плен блокировавшим пещеру превосходящими силам римлян. Воины, в составе сорока человек, стали по кругу и договорились, что каждые два воина будут убивать третьего, пока не погибнут все. При этом двое воинов, оставшихся последними в живых, должны были убить друг друга. Иосиф Флавий, командовавший этим отрядом, якобы быстро рассчитал, где нужно встать ему и его товарищу, чтобы остаться последними, но не для того, чтобы убить друг друга, а чтобы сдать крепость римлянам.
В более общей формулировке задачи участвует n воинов, стоящих по кругу, и убивают каждого m-го. Требуется определить номер k начальной позиции воина, который останется последним.
·
Лекция № 10.
Тема: графы и их способы задания
Основные вопросы, рассматриваемые на лекции:
1. Виды графов
2. Степени вершин
3. Помеченные графы
4. Изоморфизмы графов и орграфов
5. Матрицы смежности и инцидентности
Краткое содержание лекционного материала
1. Виды графов. Граф  состоит из двух множеств.
состоит из двух множеств.  . Элементы множества
. Элементы множества  называются вершинами, точками или узлами.
называются вершинами, точками или узлами.  . Неупорядоченные пары
. Неупорядоченные пары  называются ребрами, линиями или дугами.
называются ребрами, линиями или дугами.
Если  , то говорят, что ребро
, то говорят, что ребро  соединяет вершины
соединяет вершины  и
и  . При этом вершины u и v называются концами ребра
. При этом вершины u и v называются концами ребра  .
.

Диаграмма графа G=(V,E) представляется в виде точек (или кружков) на плоскости, каждая из которых изображает вершину графа. Ребро графа  изображается отрезком или дугой, соединяющей вершины u и v.
изображается отрезком или дугой, соединяющей вершины u и v.
Диаграмму графа также называют графом.

Две вершины графа u и v называются смежными, если они соединены некоторым ребром e графа. Вершина u и ребро e называются инцидентными, если u является концом ребра e. Два ребра e и f графа называются смежными, если они инцидентны одной и той вершине u графа.
(p,q)-граф – это граф с p вершинами и q ребрами
(p³1 и  ).
).
Тривиальный (p,0)-граф не содержит ни одного ребра.
Полный граф  – это
– это  -граф, содержащий все возможные ребра между
-граф, содержащий все возможные ребра между  вершинами.
вершинами.
Кроме графов (или неупорядоченных графов) рассматриваются и другие виды графов.
Мультиграф отличается от графа тем, что две вершины могут быть соединены двумя и более ребрами. При этом ребра, соединяющие две вершины в количестве двух и более, называются кратными.
Псевдограф отличается от графа тем, что в нем могут быть и кратные ребра, и петли (ребра, соединяющие вершины с самими собой).
Ориентированный граф (или орграф) G=(V,E) отличается от графа тем, что E является множеством упорядоченных пар различных вершин множества V. На диаграмме две точки орграфа соединятся не линиями, а стрелками.
В орграфах нет петель. Бинарное отношение 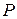 графически представляются орграфом, в котором соотношение
графически представляются орграфом, в котором соотношение  изображается петлей, а соотношения
изображается петлей, а соотношения 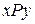 и
и  двусторонней стрелкой (объединяются две противоположно направленные стрелки).
двусторонней стрелкой (объединяются две противоположно направленные стрелки).
2. Степени вершин. Степень  вершины u – это число ребер, инцидентных вершине u. Вершина u называется изолированной (концевой), если
вершины u – это число ребер, инцидентных вершине u. Вершина u называется изолированной (концевой), если  (
( ).
).
Следующая теорема была первой в истории теории графов (1936 г.)
Теорема 1 (Л.Эйлер). Сумма степеней всех вершин ( )-графа равна удвоенному числу его ребер:
)-графа равна удвоенному числу его ребер:  .
.
Доказательство. При пересчете ребер, инцидентных всем вершинам, каждое ребро считается два раза.
Следствие. В графе число вершин с нечетными степенями четно.
Доказательство. Пусть вершины  имеют нечетные степени, а
имеют нечетные степени, а  вершины – четные степени. Тогда
вершины – четные степени. Тогда
 .
.
3. Помеченные графы. Граф называется помеченным (или перенумерованным), если его точки обозначены попарно различными пометками.
Теорема 2. Существует  помеченных графов с числом вершин n и
помеченных графов с числом вершин n и  помеченных (n,m)-графов.
помеченных (n,m)-графов.
Доказательство. Неупорядоченная пара {u,v} различных элементов u и v из множества V с числом элементов n есть сочетание без повторений из n элементов по 2. Поэтому число всех возможных ребер графа равно Cn2.
Каждый граф имеет множество ребер – некоторое подмножество множества из Cn2 элементов. Число всех подмножеств k-множества равно 2k. Число всех  -подмножеств k-множества равно
-подмножеств k-множества равно  .
.
4. Изоморфизмы графов и орграфов. Графы G1=(V1,E1) и G2=(V2,E2) называются изоморфными, если существует биекция j: V1®V2, которая сохраняет отношение смежности между вершинами графа:
"u,vÎV1 ({u,v}ÎE1Û{j(u),j(v)}ÎE2).
Пример изоморфных графов:

В этом примере биекция  является изоморфизмом графов.
является изоморфизмом графов.
Графы G1=(V1,E1) и G2=(V2,E2) могут быть неизоморфными, если:
1)  ;
;

2)  ;
;

3) для каждого  графы имеют различные числа вершин степени
графы имеют различные числа вершин степени  .
.

Графы могут быть неизоморфными, даже если все перечисленные три условия выполнены:

Орграфы G1=(V1,E1) и G2=(V2,E2) называются изоморфными, если существует биекция j: V1®V2, которая сохраняет отношение смежности между вершинами орграфа:
"u,vÎV1 ((u,v)ÎE1Û(j(u),j(v))ÎE2).
Пример. Приведем все попарно неизоморфные (3,2)-орграфы:

5. Матрицы смежности и инцидентности. Матрицей смежности графа (орграфа)  называется матрица
называется матрица  , определяемая следующим образом: для всех
, определяемая следующим образом: для всех 


Матрицы смежности представляют собой квадратные матрицы с элементами 0 и 1, у которых по главной диагонали расположены нули. Матрица смежности графа симметрична относительно главной диагонали.
Матрицей инцидентности  -графа
-графа  называется прямоугольная
называется прямоугольная  -матрица
-матрица  , определяемая следующим образом: для всех
, определяемая следующим образом: для всех 

Матрицей инцидентности  -орграфа
-орграфа  называется прямоугольная
называется прямоугольная  -матрица
-матрица  , определяемая следующим образом: для всех
, определяемая следующим образом: для всех 
