Резистивные электрические цепи и методы их расчета

 

Содержание:

Введение.

Глава 1. Электрическая цепь: основные понятия и определения.

Глава 2. Методы расчета простых резистивных цепей.

Глава 3. Расчет резистивных электрических цепей методом токов ветвей.

Глава 4. Метод узловых напряжений (МУН).

Заключение.

Используемая литература

 

Глава 1. Электрическая цепь: основные понятия и определения.

Электромагнитные процессы, протекающие в электротехнических устройствах, как правило, достаточно сложны. Однако во многих случаях, их основные характеристики можно описать с помощью таких интегральных понятий, как: напряжение, ток, электродвижущая сила (ЭДС). При таком подходе совокупность электротехнических устройств, состоящую источников и приемников электрической энергии, предназначенных для генерации, передачи, распределения и преобразования электрической энергии и (или) информации, рассматривают как электрическую цепь. Таким образом, электрическая цепь состоит из отдельных элементов (частей, объектов), соединенных соответствующим образом и выполняющих определенные функции. Основными элементами цепи являются источники и приемники электрической энергии (сигналов). Электротехнические устройства, производящие электрическую энергию, называются генераторами или источниками электрической энергии, а устройства, потребляющие ее – приемниками (потребителями) электрической энергии.

У каждого элемента цепи можно выделить определенное число зажимов (полюсов), с помощью которых он соединяется с другими элементами. К двухполюсным элементам, имеющим два зажима, относятся: большинство источников энергии, резисторы, катушки индуктивности, конденсаторы. Из многополюсных элементов наиболее распространены триоды, трансформаторы, усилители и т.д.

Большинство электрических цепей электротехнических устройств моделируют, используя базовые идеальные двухполюсные элементы, каждая из которых описывает в количественном отношении какую-либо одну из сторон реального электромагнитного процесса. Далее будут подробно изучаться такие базовые элементы, как: резистивный, индуктивный и емкостный элементы, источники сигналов, идеальный ключ и идеальный проводник.

Все элементы электрической цепи условно можно разделить на активные и пассивные. Активный элемент обязательно содержит в своей структуре источник электрической энергии. Пассивными являются элементы, в которых рассеивается (резисторы) или накапливается (катушка индуктивности и конденсаторы) энергия. К основным характеристикам элементов цепи относятся их вольт-амперные, вебер-амперные и кулон-вольтные характеристики. Если характеристики этих элементов описываются линейными уравнениями, то они называются линейными, в противном случае они относятся к классу нелинейных. Строго говоря, все элементы являются нелинейными. Однако в определенных пределах изменения переменных указанных характеристик и частот электрических сигналов можно некоторые элементы рассматривать как линейные, что существенно упрощает математическое описание и анализ процессов электрической цепи. Коэффициенты, связывающие переменные, их производные и интегралы в уравнениях элементов, называются параметрами элемента.

Цепи, содержащие только линейные элементы, называются линейными. При наличии в схеме хотя бы одного нелинейного элемента цепь считается нелинейной.

Любой элемент электрической цепи характеризуется скалярными алгебраическими величинами, которые в общем случае произвольными функциями времени 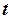, в том числе: электрическим зарядом , потокосцеплением , током 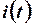и напряжением 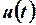, однако в практических электротехнических задачах чаще всего используют в качестве переменных только токи 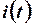и напряжения 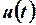, что объясняется относительным удобством физических измерений этих величин.

Электрический ток определяется как отношение:

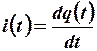, (1.1)

где , , ,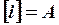

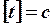а электрическое напряжение – как разность:

, (1.2)

где и 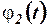− электрические потенциалы точек (полюсов) 1 и 2 соответственно, 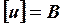, 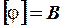(рис.1.1).

Рис.1.1. Ток и напряжение элемента электрической цепи

Знаки тока и напряжения зависят от условно выбранных на схеме положительных направлений. Направления указываются на схеме соответствующими стрелками. Различают согласованные направления и несогласованные. При согласованных направлениях тока и напряжения их стрелки совпадают.

Если электрическое напряжение 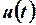определить как работу в электрическом поле:

,

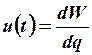то отсюда можно получить соотношение для мощности :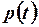

,

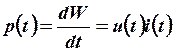где , .

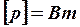Очевидно, что знак мощности 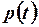зависит от знаков 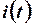и 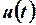. При согласованных направлениях (от одного узла) по знаку мощности можно судить о направлении передачи энергии.

Если , то элемент в данный момент времени 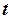потребляет энергию и является пассивным. Если , то элемент отдает мощность во внешнюю цепь, т.е. работает как источник и является активным.

Описание топологии цепи (соединений элементов) определяется законами Кирхгофа. Уравнения соединений (Кирхгофа) – это узловые и контурные уравнения топологии цепи.

.

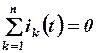Алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю для любого момента времени (рис.1.2,а).

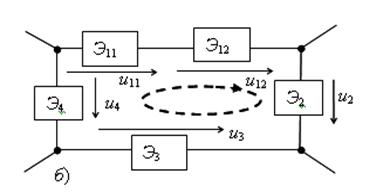
Рис.1.2.Токи в узле цепи (а) и напряжения в контуре (б)

Обычно токи, направленные к узлу, считаются положительными, а токи, направленные от узла, – отрицательными.

.

Алгебраическая сумма напряжений по замкнутому контуру (рис.1.2б) равна нулю для любого момента времени 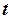. С положительными знаками принимаются слагаемые, соответствующие напряжениям, направления (полярности) которых совпадают с направлением обхода контура, а с отрицательными знаками – несовпадающие.

Например, для приведенных примеров:

(рис. 1.2а),

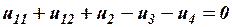(рис. 1.2б),

Характер процессов в электрической цепи зависит от топологии цепи и от типа ее элементов.

 

Глава 2. Методы расчета простых резистивных цепей.

 

2.1. Резистивный элемент: определение и особенности.

Резистивный элемент – это идеализированный двухполюсный элемент, описывающий в количественном отношении только одну сторону реального процесса – необратимое преобразование электромагнитной энергии в другие виды (потери).

Резистивный элемент полностью определяется своей вольтамперной характеристикой (ВАХ). Для линейных резистивных элементов уравнения ВАХ описываются законом Ома.

На рис.1.3. приведено условное обозначение элемента, его ВАХ и временные зависимости тока 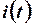и напряжения на элементе 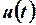, иллюстрирующие основное свойство элемента.

 

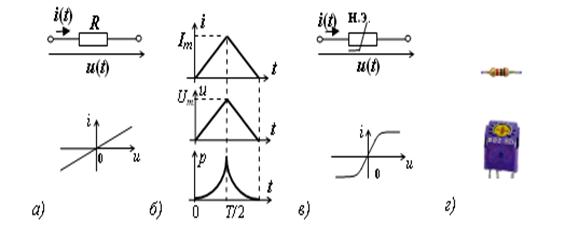
Рис.1.3. Резистивный элемент: а - обозначение линейного элемента и его ВАХ, б – временные зависимости , и для линейного резистора, в – нелинейный резистивный элемент и его ВАХ, г – варианты конструктивного исполнения резисторов

Уравнение элемента связывает ток 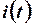, протекающий по элементу и напряжение 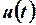на полюсах элемента.

Для резистивного элемента уравнения элемента и ВАХ совпадают:

,

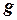где – сопротивление, – проводимость резистора, 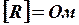, , 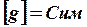и параметры элемента .

Параметры и 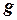являются константами и имеют смысл только для линейных резисторов.

Функциональные уравнения ВАХ нелинейного резистора (уравнения элемента) можно записать в виде нелинейных зависимосте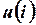й или 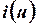. Эти зависимости могут быть представлены в различных формах, например, графически, в виде таблицы либо приближенными аналитическими выражениями.

Мощность в линейном резисторе определяется выражением

.

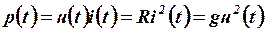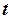Отсюда следует, что для любых значений . Следовательно, резистор потребляет электромагнитную энергию, т.е. он пассивен.

Выражения (1.7) и (1.8) позволяют сделать вывод о совпадении на линейном резисторе формы тока 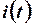и формы напряжения 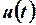с точностью до масштабных коэффициентов и .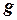

Это важнейшее свойство линейного резистивного элемента широко используется в электротехнической практике: линейный резистор – весьма удобный датчик тока (преобразователь тока в напряжение).

Наиболее близким реальным прототипом к линейному резистивному элементу можно считать проволочное сопротивление.

Простыми резистивными цепями называют такие цепи, элементы которых (резисторы) соединены или только последовательно, или только параллельно, или только последовательно и параллельно.

Параллельное (последовательное) соединение нескольких однотипных элементов может быть заменено одним элементом. Поэтому простую цепь с одним источником путем объединения элементов, включенных только параллельно или только последовательно, можно свести к цепи, содержащей лишь один элемент. Резистивные цепи, которые указанным путем не могут быть к одному элементу активного резистора, называются сложными.

Расчет простых резистивных цепей с одним источником производится с использованием закона Ома. При наличии нескольких источников используется метод наложения.

2.2. Параллельные цепи

Пусть электрическая цепь содержит два резистора и источник тока:

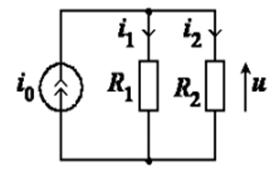
Определим напряжение в цепи и токи в ветвях, если известны величины сопротивлений резисторов и ток источника. Учитывая заданное направление тока 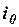и выбранные направления токов и , составляем уравнение по ЗКТ:

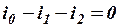, откуда .

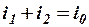Так как для токов и напряжения выбрана согласованная система отсчета, то

; .

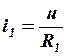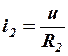Тогда

Следовательно, эквивалентное сопротивление двух параллельно соединенных резисторов определяется из соотношения:

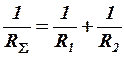
и равно отношению произведения соединяемых резисторов к их сумме:

.

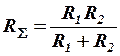Напряжение цепи находится как произведение тока источника на эквивалентное сопротивление

.

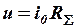Токи в ветвях вычисляются по закону Ома:

; .

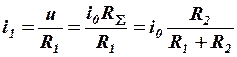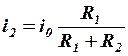Таким образом, выведено правило деления тока между двумя ветвями (или просто правило деления тока): ток в данной ветви пропорционален отношению сопротивления соседней ветви к сумме сопротивлений обеих ветвей.

Если использовать проводимости ветве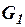й и 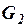, то правило деления тока можно записать так:

; .

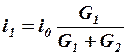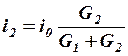Таким образом, ток в данной ветви пропорционален проводимости этой ветви к сумме проводимостей ветвей. Последнее соотношение можно объединить в одно:

,

где 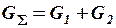− эквивалентная проводимость цепи.

Аналогично можно доказать, что для параллельно соединенных резисторов:

.

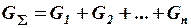2.3. Последовательные цепи