Критерии СТЬЮДЕНТА

Чтобы оценить существенность параметров, необходимо рассчитать для них критерии Стьюдентаt_a, t_b, t_r. Для параметров а, b и коэффициента r_xy критерий Стьюдента определяет соотношение между самим параметром и его ошибкой;

Для коэффициента корреляции формулу расчета критерия Стьюдента можно преобразовать и она будет иметь несколько иной вид:

Фактические значения критерия Стьюдента сравниваются с табличными при определенном уровне надежности α и числе степеней свободы df= (п—2). По результатам этого сравнения принимаются или отвергаются нулевые гипотезы о несущественности параметров или коэффициента корреляции. Если фактическое значение критерия Стьюдента больше табличного, тогда гипотеза о несущественности отвергается. Подтверждение существенности коэффициента регрессии равнозначно подтверждению существенности уравнения регрессии в целом.

Ошибки аппроксимации.

Практически всегда фактическое значение результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии. Чем меньше эти отличия, тем ближе будут теоретические значения подходить к эмпирическим следовательно, тем лучше подобрано уравнение регрессии Величина отклонений фактических значений от расчетных результативного признака по каждому наблюдению представляет собой ошибку аппроксимации.

Ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю:

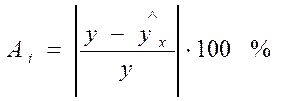
Эти ошибки уже поддаются сравнению, но они оценивают каждое наблюдение в отдельности. Такую ошибку принято называть относительной ошибкой аппроксимации.

Чтобы оценить качество модели в целом, можно определить среднюю ошибку аппроксимации, представляющую собой среднюю арифметическую относительных ошибок аппроксимации по всем наблюдениям, включаемым в модель: