Теорема Пуассона
Обозначим  — вероятность того, что в серии из
— вероятность того, что в серии из 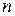 испытаний Бернулли с вероятностью успеха
испытаний Бернулли с вероятностью успеха  ровно
ровно  раз произойдет успех. Рассмотрим асимптотическое поведение вероятностей
раз произойдет успех. Рассмотрим асимптотическое поведение вероятностей  при условии, что
при условии, что  ограничено. Это возможно в случае, когда либо
ограничено. Это возможно в случае, когда либо  , либо
, либо  . Не умаляя общности, достаточно рассмотреть случай:
. Не умаляя общности, достаточно рассмотреть случай:  и
и  , тогда
, тогда  .
.
Теорема. Пусть  при
при  , причем так, что
, причем так, что  , где
, где  . Тогда для любого
. Тогда для любого 
 . (1).
. (1).
Доказательство. Поскольку по предположению  , то для любого фиксированного
, то для любого фиксированного  достаточно больших
достаточно больших 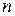
 .
.
Но

и
 ,
,
что и доказывает (1).
ДЛЯ СТАТИСТИКОВ
Метод моментов
В математической статистике — это один из первых общих методов нахождений оценок неизвестных параметров по результатам наблюдений. Карл Пирсон использовал его при решении задачи аппроксимации эмпирических распределений с помощью системы распределений Пирсона в 1894 году.
Так как в силу теоремы Гливенко эмпирическая функция распределения  близка в равномерной метрике к
близка в равномерной метрике к  , то естественно предполагать, что выборочные моменты, вычисленные по эмпирической функции распределения, будут близки к соответствующим теоретическим.
, то естественно предполагать, что выборочные моменты, вычисленные по эмпирической функции распределения, будут близки к соответствующим теоретическим.
Именно на этом и основан метод моментов. И так, пусть  выборка объема
выборка объема 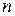 из параметрического семейства распределений
из параметрического семейства распределений  , где
, где  . Выберем некоторую борелевскую функцию
. Выберем некоторую борелевскую функцию  , такую чтобы существовал момент
, такую чтобы существовал момент

и к тому же, что бы существовала функция  , обратная к функции
, обратная к функции  в области
в области  . В качестве оценки метода моментов
. В качестве оценки метода моментов  для истинного значения неизвестного параметра
для истинного значения неизвестного параметра  возьмем решение уравнения
возьмем решение уравнения
 ,
,
то есть в качестве оценки мы выбираем такое число, чтобы теоретический момент совпадал с выборочным при данной реализации выборки.
Чаще всего в качестве функции  выбирают
выбирают  , то есть начальные теоретические моменты приравниваются к соответствующим выборочным. Понятно, что, если параметр одномерный, то достаточно одного уравнения. Если же параметр
, то есть начальные теоретические моменты приравниваются к соответствующим выборочным. Понятно, что, если параметр одномерный, то достаточно одного уравнения. Если же параметр 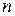 –мерный, то необходимо решить систему
–мерный, то необходимо решить систему 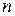 уравнений.
уравнений.
Пример. Дана выборка  из распределения с плотностью
из распределения с плотностью  ,
,  ,
,  . Найти методом моментов оценку для параметра
. Найти методом моментов оценку для параметра  .
.
Решение. Вычислим математическое ожидание  . Оценку
. Оценку  найдем как решение уравнения
найдем как решение уравнения  . Таким образом, оценка метода моментов в данном случае имеет вид
. Таким образом, оценка метода моментов в данном случае имеет вид  .
.
Замечание. В том случае, если корень уравнения  , в то время как
, в то время как  . Тогда оценку необходимо откорректировать. Для этого в качестве оценки метода моментов берут ближайшую к
. Тогда оценку необходимо откорректировать. Для этого в качестве оценки метода моментов берут ближайшую к  точку из
точку из  или его замыкания.
или его замыкания.
Пример. Дана выборка  из нормального распределения с параметрами
из нормального распределения с параметрами  с неотрицательным средним
с неотрицательным средним  . В этом случае оценка метода моментов для неизвестного среднего имеет вид
. В этом случае оценка метода моментов для неизвестного среднего имеет вид  . На практике может случиться так, что
. На практике может случиться так, что  , поэтому в таком случае в качестве оценки метода моментов разумнее выбрать 0. Следовательно, скорректированная оценка метода моментов имеет вид
, поэтому в таком случае в качестве оценки метода моментов разумнее выбрать 0. Следовательно, скорректированная оценка метода моментов имеет вид  .
.
Замечание. Оценки метода моментов определяются неоднозначно. Вообще говоря, выбирая различные функции  , получим разные оценки
, получим разные оценки  для неизвестного параметра
для неизвестного параметра  .
.
| Теорема. | Пусть  — оценка метода моментов неизвестного параметра, причем функция — оценка метода моментов неизвестного параметра, причем функция  непрерывна. Тогда непрерывна. Тогда  сильно состоятельна. сильно состоятельна.
|
Доказательство. Согласно теореме Колмогорова (усиленный закон больших чисел для одинаково распределенных случайных величин)
 .
.
Поскольку функция  непрерывна, то и
непрерывна, то и
 .
.
Метод максимального правдоподобия
Согласно методу максимального правдоподобия в качестве оценок выбираются те значения параметров, при которых данные результаты наблюдения «наиболее вероятны».
| Определение | Функцию
 назовем обобщенной плотностью. назовем обобщенной плотностью.
|
Функция, фигурирующая в последнем определении, является плотностью относительно меры Лебега для абсолютно непрерывного распределения и плотностью относительно считающей меры для дискретного распределения.
| Определение | Пусть выборка из распределения выборка из распределения  с плотностью с плотностью  , тогда случайная функция , тогда случайная функция
 называется функцией правдоподобия.
называется функцией правдоподобия.
|
| Определение | Оценкой максимального правдоподобия  неизвестного параметра неизвестного параметра  называется то значение называется то значение  , при котором функция правдоподобия достигает своего максимума, то есть решение уравнения правдоподобия , при котором функция правдоподобия достигает своего максимума, то есть решение уравнения правдоподобия
 . .
|
Замечание Решая уравнение правдоподобия  ,необходимо отбросить все корни, которые имеют вид
,необходимо отбросить все корни, которые имеют вид  , то есть не зависят от выборки
, то есть не зависят от выборки  .
.
Так как положительная функция достигает своего максимума в той же точке, что и ее логарифм, то на практике для анализа часто используют натуральный логарифм функции правдоподобия.
| Определение | Случайную функцию
 называют логарифмической функцией правдоподобия.
называют логарифмической функцией правдоподобия.
|
Пример Дана выборка  из показательного распределения с плотностью
из показательного распределения с плотностью  ,
,  ,
,  . Методом максимального правдоподобия найти оценку параметра
. Методом максимального правдоподобия найти оценку параметра  .
.
Решение. Функция правдоподобия в данном случае имеет вид:  , если все
, если все  и
и  в противном случае.
в противном случае.
Соответственно ее логарифм
 .
.
Решим уравнение правдоподобия
 ,
,
или после дифференцирования
 .
.
Решением последнего уравнения является:
 .
.
Так как  и
и  , то точка
, то точка  является точкой максимума функции правдоподобия и, следовательно,
является точкой максимума функции правдоподобия и, следовательно,  является оценкой максимального правдоподобия.
является оценкой максимального правдоподобия.
Пример. Дана выборка  из распределения Пуассона
из распределения Пуассона  . Методом максимального правдоподобия найти оценку параметра
. Методом максимального правдоподобия найти оценку параметра  .
.
Решение. В данном случае функция правдоподобия имеет вид:
 ,
,
логарифмируя ее, получим
 .
.
Решением уравнения правдоподобия  является:
является:

Следовательно, оценка максимального правдоподобия имеет вид
Неравенство Крамера–Рао
Пусть  — выборка из распределения, принадлежащего параметрическому семейству
— выборка из распределения, принадлежащего параметрическому семейству  , здесь
, здесь  .
.
Определение. Множество  , такое, что при всех
, такое, что при всех  выполняется равенство
выполняется равенство  , назовем носителем семейства распределений
, назовем носителем семейства распределений  .
.
Замечание. Носитель распределения в этом смысле определяется не единственным образом, но все носители отличаются на множество нулевой вероятности.
Определение.Семейство распределений  назовем регулярным, если существует носитель
назовем регулярным, если существует носитель  семейства распределений
семейства распределений  такой, что при каждом
такой, что при каждом  функция
функция  непрерывно дифференцируема по
непрерывно дифференцируема по  во всех точках
во всех точках  .
.
Замечание . Вместо непрерывной дифференцируемости  можно требовать того же от
можно требовать того же от  .
.
Пусть  — выборка из распределения, принадлежащего параметрическому семейству
— выборка из распределения, принадлежащего параметрическому семейству  , где
, где  .
.
Определение. Величина  если она существует, называется информацией Фишера в одном наблюдении.
если она существует, называется информацией Фишера в одном наблюдении.
Справедливо следующее утверждение.
Теорема 24.1. (Неравенство Крамера–Рао). Пусть семейство распределений  удовлетворяет условию регулярности (см. определение24.2) и информация Фишера существует, положительна и непрерывна по
удовлетворяет условию регулярности (см. определение24.2) и информация Фишера существует, положительна и непрерывна по  во всех
во всех  . Тогда для любой несмещенной оценки
. Тогда для любой несмещенной оценки  , дисперсия которой
, дисперсия которой  ограничена на любом компакте в области
ограничена на любом компакте в области  , справедливо неравенство
, справедливо неравенство  .
.
Докажем предварительно утверждение.
Лемма. В условиях теоремы 24.1 для любой статистики  ,
,  , дисперсия которой ограничена на компактах, имеет место равенство
, дисперсия которой ограничена на компактах, имеет место равенство
 .
.
Доказательство леммы..

Через  в интегралах обозначен вектор
в интегралах обозначен вектор  .
.
Доказательство неравенства Крамера–Рао.
Пусть  . Тогда
. Тогда

Поскольку  , то
, то  и
и
 (1)
(1)
Пусть теперь  , то есть
, то есть  . Тогда
. Тогда
 (2)
(2)
Так как  , то из (1) и (2) вытекает
, то из (1) и (2) вытекает
 (3)
(3)
Найдем  :
:
 .
.
подставляя дисперсию в неравенство (3) получим
 или
или  , что и требовалось доказать.
, что и требовалось доказать.
| Теорема неравенство Крамера–Рао для смещенных оценок | Пусть семейство распределений  удовлетворяет условию регулярности, информация Фишера существует, положительна и непрерывна по удовлетворяет условию регулярности, информация Фишера существует, положительна и непрерывна по  во всех во всех  . Тогда для любой оценки . Тогда для любой оценки  , дисперсия которой , дисперсия которой  ограничена на любом компакте в области ограничена на любом компакте в области  , справедливо неравенство , справедливо неравенство
 или или  . .
|
| Следствие. | Пусть семейство распределений  удовлетворяет условиям теорем, и оценка удовлетворяет условиям теорем, и оценка  такова, что в неравенстве Крамера–Рао достигается равенство: такова, что в неравенстве Крамера–Рао достигается равенство:
 или или  ,
тогда оценка эффективна в классе ,
тогда оценка эффективна в классе  . .
|
Доверительный интервал дляля математического ожидания при известной дисперсии
Пусть  — выборка из нормального распределения с параметрами
— выборка из нормального распределения с параметрами  . Статистика
. Статистика  имеет распределение
имеет распределение  .
.
Действительно, введем в рассмотрение центрированные нормированные случайные величины  , которые имеют стандартное нормальное распределение. Тогда
, которые имеют стандартное нормальное распределение. Тогда  , а последняя сумма как нетрудно видеть распределена по нормальному закону со средним нуль и дисперсией единица, так как
, а последняя сумма как нетрудно видеть распределена по нормальному закону со средним нуль и дисперсией единица, так как
а) линейная комбинация нормальных случайных величин есть нормальная величина;
б)  ;
;
в)  .
.
Следовательно  , где
, где  квантиль стандартного нормального распределения уровня
квантиль стандартного нормального распределения уровня  , то есть решение уравнения
, то есть решение уравнения  . Тогда
. Тогда
 . .
|
Для математического ожидания при неизвестной дисперсии
В качестве статистики для построения этого доверительного интервала выберем , которая имеет
, которая имеет  –распределение с
–распределение с  степенью свободы.
степенью свободы.
Введем в рассмотрение центрированные нормированные случайные величины  , которые имеют стандартное нормальное распределение.
, которые имеют стандартное нормальное распределение.
1. , а последняя сумма как нетрудно видеть распределена по нормальному закону со средним нуль и дисперсией единица, так как
, а последняя сумма как нетрудно видеть распределена по нормальному закону со средним нуль и дисперсией единица, так как
а) линейная комбинация нормальных случайных величин есть нормальная величина;
б)  ;
;
в)  .
.
2. Определим случайные величины  как результат воздействия на
как результат воздействия на  ортогонального преобразования, следующего вида
ортогонального преобразования, следующего вида
 ,
,  ,
,
 .
.
Тогда

А так как все  ,
,  имеют стандартное нормальное распределение и независимы, то по определению сумма
имеют стандартное нормальное распределение и независимы, то по определению сумма  имеет
имеет
 –распределение с
–распределение с  степенью свободы.
степенью свободы.
Так как случайные величины  ,
,  независимы, и
независимы, и  зависит только от
зависит только от  ,
,  и не зависит от
и не зависит от  , то и величины
, то и величины  ,
,  независимы.
независимы.
3. Далее
 ,
,
в силу независимости случайных величин  ,
,  по определению дробь
по определению дробь  имеет
имеет  –распределение с
–распределение с  степенью свободы.
степенью свободы.
Таким образом, с учетом того, что распределение Стьюдента симметрично имеем  , здесь
, здесь  квантиль
квантиль  –распределения с
–распределения с  степенью свободы уровня
степенью свободы уровня  . Откуда получаем доверительный интервал
. Откуда получаем доверительный интервал
 . .
|