Верна и обратная теорема.
Теорема 5.3.2.если функцию  можно представить как сумму числа А и бесконечно малой величины
можно представить как сумму числа А и бесконечно малой величины  при
при  , то число А есть предел этой функции при
, то число А есть предел этой функции при  , т.е.
, т.е.  .
.
По условию  , пусть при
, пусть при  . Так как функция
. Так как функция  есть бесконечно малая величина при
есть бесконечно малая величина при  , то для любого числа
, то для любого числа  >0 существует такое число
>0 существует такое число 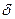 >0 , что для всех
>0 , что для всех  и удовлетворяющий условию
и удовлетворяющий условию  <
<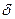 верно неравенство
верно неравенство  <
< Это и означает , что
Это и означает , что 
Примеры.Вычислить пределы.
1. 
2.  , т.к. функция
, т.к. функция  представлена в виде суммы двух слагаемых: одно постоянное равное 2, а второе бесконечно малое как произведение бесконечно малой
представлена в виде суммы двух слагаемых: одно постоянное равное 2, а второе бесконечно малое как произведение бесконечно малой  и ограниченной величины
и ограниченной величины 
Замечание. Теорема 5.3.2 может пониматься как один из признаков существования пределов функции(см. далее).