Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.
Произведение бесконечно малых величин есть величина бесконечно малая.
Произведение бесконечно малой величины на ограниченную функцию (в том числе на постоянную, на другую бесконечно малую) есть величина бесконечно малая.
Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
Свойства бесконечно малых величин.
В качестве примера докажем свойство 1 для двух бесконечно малых величин 
при 
. Покажем, что функция 
также является бесконечно малой при .
По условию есть бесконечно малые величины при . Это означает, что для любого 
>0 найдутся такие числа 
>0, 
>0 что для всех 
и удовлетворяющий условиям:
< (5.3.3)
< (5.3.4)
Выполняются соответственно неравенства
<
(5.3.5)
< (5.3.6)
Если взять в качестве числа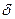 
минимальное из чисел и , т.е. 
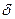, то неравенству <будут удовлетворять решения обоих неравенств (5.3.3) и (5.3.4) и следовательно, одновременно будут верны неравенства (5.3.5) и (5.3.6). Складывая почленно неравенства (5.3.5) и (5.3.6), получаем , что 
<
.
Используя свойство абсолютных величин 
, придем к более сильному неравенству <
Итак, для любого 
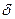>0, существует такое >0 что для всех и удовлетворяющих условию <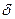, верно неравенство (5.3.7). А это и означает, что функция 
есть величина бесконечно малая.
Примеры. Даны функции:
; 
-бесконечно малая
; 
-бесконечно малая
- всюду ограничена, значит, и при 
; 
Тогда в соответствии со свойствами бесконечно малых следует 
- бесконечно малая (свойство1), при 
т.е. 
- бесконечно малая при (свойство2), т.е. 
- бесконечно малая при (свойство4) т.е. 
Замечание к свойству 4. Предел частного двух бесконечно малых представляет собой неопределенное выражение, т.е к 
не может быть применено свойство 4.
Если=0, то говорят, что есть величина бесконечно малая более высокого порядкамалости, чем ; (или - бесконечно малая более низкого порядка малости,чем ).
Если=А
0, то говорят, что и бесконечно малые одного порядка.
Если=1, и называют эквивалентными бесконечно малыми.