Бесконечно малые величины.

Бесконечно малые и бесконечно большие величины и их свойства.

Определение. Функция α(х) называется бесконечно малой величинойпри или при , если её предел равен нулю: .

Зная определение предела функции при и , можно дать развернутое определение бесконечно малой величины.

 

Определение.Функция α(х) называется бесконечно малой величинойпри , если для любого, даже сколь угодно малого положительного числа >0, найдется такое положительное число 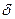>0(зависящее от ), что для всех х , не равных и удовлетворяющих условию <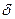(5.3.1) будет верно неравенство <(5.3.2)

 

С помощью логических символов приведем это определение к виду:

 

(α (х)- бесконечно малая величина при , или )

>0)(>0) (<) <

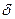Аналогично можно сформулировать определение бесконечно малой величины при , если основное неравенство (5.4) рассматривать для достаточно больших х. приводим его в краткой форме:

(α (х)- бесконечно малая величина при , или )

>0)(>0) (>S) < .

Например, функции y=cos x при и при есть бесконечно малые величины, ибо их пределы равны нулю.

Не следует путать бесконечно малую переменную и величину α (х) с очень малым, но постоянным числом>0 .

Во-первых, бесконечно малая величина – это переменная величина, в то время, как сколь угодно малая величина >0- это фиксированное постоянноечисло.

Отдельные значения бесконечно малой могут быть достаточно большими. Существенно лишь то, что по мере приближения (или ) функция α (х) в соответствии с (5.4) окажется меньше числа Т.е. α (х) может быть меньше заданного достаточно малого числа в процессе.

Пример. Рассмотрим функцию при .

;…, ;

Видим, что отдельные значения функции достаточно велики: и т.д.

Покажем, что может стать по модулю меньше числа>0.

<, если >или >, но , т.е. >откуда >. При таких значениях х функция<. Например , если , то<, если >