Примеры.
1. 
 - монотонно убывающая и ограниченная;
- монотонно убывающая и ограниченная;
2.  : 2,
: 2,  ,
,  ,…,
,…,  ,…- монотонно возрастающая и неограниченная;
,…- монотонно возрастающая и неограниченная;
3.  -1, 1, -1, 1…- немонотонная и ограниченная;
-1, 1, -1, 1…- немонотонная и ограниченная;
4.  -1,
-1,  , -
, - ,
,  ,…- немонотонная и ограниченная;
,…- немонотонная и ограниченная;
5.  0,
0,  ,
,  ,
,  ,
,  ,
,  ,
, 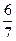 ,…
,…
Изобразим последовательность (пример 5) на числовой прямой (рис.5.1.2)

Рис. 5.1.2
 На рис.5.1.2 видно, сто с ростомn члены последовательности приближаются к единице,т.е. величина
На рис.5.1.2 видно, сто с ростомn члены последовательности приближаются к единице,т.е. величина 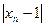 становятся все меньше и меньше. Иными словами, если рассмотреть любую сколь угодно малую окрестность числа а=1, в этой окрестности накапливается бесчисленное множество членов последовательности
становятся все меньше и меньше. Иными словами, если рассмотреть любую сколь угодно малую окрестность числа а=1, в этой окрестности накапливается бесчисленное множество членов последовательности 
 , начиная с некоторого номера N.
, начиная с некоторого номера N.
Определение.Число аназывается пределом числовой последовательности , 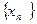 ,если для любого, сколь угодно малого числа
,если для любого, сколь угодно малого числа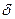 , найдется такой номер N(зависящий от
, найдется такой номер N(зависящий от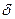 ), что для всех членов последовательности с номерами n> N,
), что для всех членов последовательности с номерами n> N,
выполняется неравенство  <
<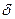
В этом случае записывают:
  
|
|
|
Если последовательность имеет предел, она называется сходящейся,в противном случае - расходящейся.
Для пределов числовой последовательности имеют место следующие теоремы (свойства).
Теорема 5.1.1. Если последовательность 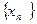 имеет предел, то только один.
имеет предел, то только один.
Доказательство.Пусть  . Предположим, существует
. Предположим, существует  . По условию для
. По условию для  >0
>0  ,
,  <
<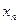 <
<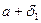 по предположению для
по предположению для  >0
>0 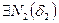 n>
n>
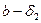 <
<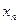 <
<
Пусть выбранные окрестности не пересекаются.











а-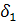
 а а+
а а+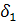 b-
b-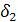 b
b  b+
b+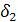
Рис.5.1.2
Если N=max 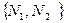 ,то для n> N один и тот же член одновременно находится в двух разных окрестностях. Следовательно, если
,то для n> N один и тот же член одновременно находится в двух разных окрестностях. Следовательно, если  , то число b не может быть пределом данной последовательности.
, то число b не может быть пределом данной последовательности.
Теорема 5.1.2. Предел постоянной величины равен самой постоянной.
Если считать, что  ,
, 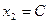 ,…,
,…,  , то, начиная уже с первого члена последовательности (n≥1), все члены последовательности лежат в окрестности точки С (совпадают с числом С), т.е.
, то, начиная уже с первого члена последовательности (n≥1), все члены последовательности лежат в окрестности точки С (совпадают с числом С), т.е.  .
.
Теорема 5.1.3. Предел положительной последовательности (переменной) неотрицательный; предел отрицательной последовательности (переменной) не положителен.
Доказательство. а) Пусть при 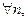
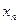 >0 и
>0 и 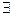
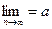 . Предположим, что а<0. по определению предела для
. Предположим, что а<0. по определению предела для  >0
>0  , что для n>N
, что для n>N 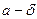 <
<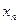 <
<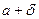 . Но это означает, что существуют отрицательные члены последовательности, что противоречит условию. Следовательно, если
. Но это означает, что существуют отрицательные члены последовательности, что противоречит условию. Следовательно, если 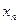 >0, то
>0, то  .
.
 |  |  |  | ||||||
 | |||||||||
 а-δ а
а-δ а  а+δ 0
а+δ 0
б) Если  <0, доказательство аналогично.
<0, доказательство аналогично.
Теорема 5.1.4. Если 
 и
и 
Доказательство.Если 

 >0
>0  , n>
, n> выполняется условие
выполняется условие <
<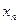 <
<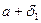 . Если
. Если 

 >0
>0  , такой, что для n>
, такой, что для n> выполняется условие
выполняется условие 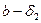 <
< <
< . Предположим, a>b (рис.5.1.4)
. Предположим, a>b (рис.5.1.4)








 n>
n> n>
n>
b-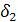
 b b+
b b+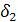 а-
а-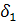 а
а  а+
а+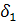 х
х
Рис.5.1.4
Если окрестности не пересекаются (всегда можно их выбрать такими), то для n>N =max 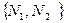 ,
,  <
<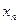 , что противоречит условию. Значит, наше предположение невернои
, что противоречит условию. Значит, наше предположение невернои  .
.
Замечание. Из теорем 5.1.3 и 5.1.4 следует: при переходе к пределам в неравенствах знак неравенства сохраняется.
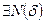 , n>N
, n>N