ПРЕДСТАВЛЕНИЕ ЧИСЛОВЫХ ДАННЫХ В КОМПЬЮТЕРНЫХ СИСТЕМАХ

 

Система вещественных чисел, используемая в ручных расчетах, предполагается бесконечной и непрерывной, т.е. отсутствуют ограничения на диапазон используемых чисел и точность (количество значащих цифр).

Пояснение: для любого вещественного числа существует бесконечно много чисел, которые больше или меньше его, и между любыми двумя вещественными числами находится также бесконечно много чисел.

В компьютерной технике размеры устройств ограничены. Эти ограничения касаются диапазона чисел и точности их представления. Поэтому система машинных чисел является конечной и дискретной, образуя подмножество системы вещественных чисел.

На рис. 3.1 схематически представлена система машинных чисел где (Xmax) и (Xmin) - соответственно максимально и минимально представимые числа, между которыми находится конечное множество допустимых чисел.

 

 

 

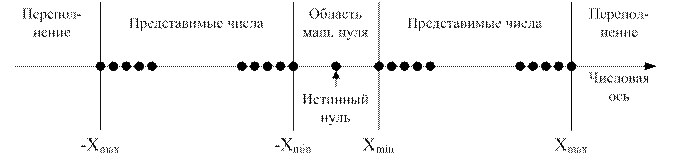
Рисунок 3.1 - Система машинных чисел

 

Если результат операции по модулю превышает |Xmax|, то возникает переполнение (overflow). Если модуль результата |X|<|Xmin|, фиксируется антипереполнение (underflow). В этом случае большинство компьютеров возвращают в качестве результата операции (0). Поэтому область чисел от

(-Xmin до Xmin), за исключением истинного нуля, называют машинным нулем. В современных универсальных компьютерных системах преимущественно используют две формы представления чисел:

- с фиксированной запятой (фиксированной точкой - fixed point) - естественная форма;

- с плавающей запятой ( плавающей точкой - floating point) - альтернативные названия - нормальная, экспоненциальная, научная запись или полулогарифмическая.

Например, пусть задано число:

 

. (3.1)

 

 

где: Х - некоторое число;

- цифры слева от запятой;

- цифры справа от запятой.

 

В позиционной системе счисления с основанием (2) его можно записать в виде:

 

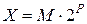. (3.2)

 

где: Х - некоторое число;

M - мантисса;

2 - основание системы счисления;

P - порядок.

 

Если каждому числу (X) в компьютерной системе однозначно соответствует мантисса (M), а порядок (Р) фиксирован для всех чисел, то число (X) представлено в форме с фиксированной запятой. Порядок (Р) в этом случае устанавливается заранее при подготовке задачи к решению, причем число (2-P), по существу, является масштабным коэффициентом, на который необходимо умножить исходные данные для того, чтобы избежать переполнения разрядной сетки.

Естественная форма характеризуется тем, что положение разрядов (и запятой) в машинном представлении чисел остается всегда постоянным независимо от величин чисел, с которыми оперирует компьютерная система. С целью упрощения процедуры определения масштабных коэффициентов запятую обычно фиксируют перед старшим разрядом мантиссы или после ее младшего разряда.

В первом случае компьютерная система оперирует с числами, которые по абсолютной величине меньше единицы, то есть, с правильными дробями. Если количество разрядов для представления мантиссы равно (n), то: (|Xmin|=2-n, |Xmax|=1-2-n).

Во втором случае компьютерная система выполняет операции с целыми числами, абсолютные величины которых находятся в пределах от (1 (минимального, не равного нулю числа) до 2n-1).

Если каждому числу (X) однозначно соответствует пара (М) и (Р), то такое представление называют формой с плавающей запятой. Следует иметь в виду, что положение запятой в реальной разрядной сетке компьютерной системы физически никак не указывается, а только "подразумевается" и само число можно записать в виде:

 

. (3.3)

. (3.4)

 

где: Х - некоторое число;

М - мантисса числа (Х);

Е - разделитель мантиссы и порядка числа (Х);

Р - порядок числа (Х).

 

Для однозначного представления числа в нормальной форме принято, что мантисса должна удовлетворять условию:

 

. (3.5)

 

то есть мантисса должна быть правильной дробью, а ее старшая цифра — отличной от (0). В таком случае представление числа является нормализованным. Помимо однозначного представления, это дает еще и сохранение максимального количества значащих цифр мантиссы при выполнении операций. Положение разрядов числа в форме с плавающей запятой не является постоянным, то есть запятая как бы плавает.

С учетом рассмотренных ранее структурных единиц информации, различают несколько форматов данных с фиксированной запятой. Например, в компьютерах IBM PC AT машинное слово имеет длину 16 бит (2 байта).

Используются следующие форматы: слово, полуслово (байт), двойное слово (doubleword), учетверенное слово (quadword).

В соответствии с перечисленными форматами различают базовые типы целочисленных данных:

- слово – 8 бит;

- целое слово - 16 бит;

- короткое целое слово - 32 бит;

- длинное целое слово - 64 бит.

Для того, чтобы компьютерная система могла оперировать как положительными, так и отрицательными числами, в разрядную сетку машинного представления числа необходимо ввести знаковую часть.

В двоичной системе счисления принято знак положительного числа обозначать «0», а знак отрицательного числа - «1» (обычно это крайний левый бит в представлении числа), как показано на рис.3.2.

 

Рисунок 3.2 - Формат числа в двоичной системе счисления со знаковым битом

 

Будем обозначать целые знаковые числа в виде:

 

. (3.6)

 

а правильные дроби:

 

. (3.7)

 

В связи с тем, что алгоритмы выполнения операций в компьютерных системах имеют свою специфику, возникает проблема представления отрицательных чисел.

Ее решают за счет использования особых способов кодирования числовых данных.

Рассмотрим три наиболее распространенных кода, которые применяются на практике: - прямой код; - обратный код; - дополнительный код.

Прямой код используется для представления отрицательных чисел в запоминающем устройстве компьютерной системы, а также при умножении и делении.

Обратный и дополнительный коды используются для замены операции вычитания операцией сложения, что упрощает устройство арифметического блока компьютерной системы.

К кодам выдвигаются следующие требования:

- разряды числа в коде жестко связаны с определенной разрядной сеткой;

- для записи кода знака в разрядной сетке отводится фиксированный, строго определенный разряд.

1. Прямой код. Наиболее естественный код. Формируется следующим образом: в знаковый бит (SX) числа помещают знак числа (0 - если число положительное и 1 - если число отрицательное ), а остальные биты используют для абсолютного значения (модуля) числа. Правило преобразования чисел в прямом коде можно записать так:

 

. (3.8)

 

где A - вес старшего разряда в n-разрядной сетке, A=2s-1.

 

Отображение s-битных наборов ( прямой код верхняя числовая прямая) на числовую ось ( числа нижняя числовая прямая ) для компьютерной системы показано на рис. 3.3

 

 

Рисунок 3.3- Отображение s-битных наборов (прямой код ) на числовую ось

 

Например:

 

Десятичное число Двоичное число Прямой код Комментарии
(0(10)) 0000(2) 0,000 положительный (0)
(0(10)) 0000(2) 1,000 отрицательный (0)
(4(10)) 0100(2) 0,100 положительная (4)
(- 4(10)) 1100(2) 1,100 отрицательная (4)
(3(10)) 0011(2) 0,011 положительная (3)
(- 3(10)) 1011(2) 1,011 отрицательная (3)

 

Диапазон представимых чисел: -(2s-1-1)…(2s-1).

Положительный момент заключается в удобстве операции ввода-вывода данных. Отрицательный момент в том, что существует два представления (0) и операция алгебраического сложения требует анализа знаков и модулей операндов, и выбора фактической операции сложения или вычитания.

2. Обратный код.Обратный ( n - разрядный ) двоичный код положительного целого числа состоит из одноразрядного кода знака (0), за которым следует ( n - 1) разрядное двоичное представление модуля числа, то есть обратный код для положительного числа совпадает с прямым кодом.

Обратный ( n - разрядный ) двоичный код отрицательного целого числа состоит из одноразрядного кода знака (1), за которым следует ( n - 1) разрядное двоичное число, представляющее собой инвертированное (n - 1) разрядное представление модуля числа, то есть для отрицательного числа все цифры числа заменяются на противоположные, а именно ( 1 на 0, а 0 на 1) и в знаковый разряд заносится единица.

Обратный код числа определяется соотношением:

 

. (3.9)

 

где B=2s-1=Xmax - максимальное число в n-разрядной сетке.

 

Отображение s-битных наборов ( обратный код верхняя числовая прямая) на числовую ось ( числа нижняя числовая прямая ) для компьютерной системы показано на рис. 3.4.

 

 

Рисунок 3.4 - Отображение s-битных наборов (обратный код ) на числовую ось

 

Например:

 

Десятичное число Двоичное число Обратный код Комментарии
(0(10)) 0000(2) 0,000 положительный (0)
(0(10)) 1111(2) 1,111 отрицательный (0)
(4(10)) 0100(2) 0,100 положительная (4)
(- 4(10)) 1011(2) 1,011 отрицательная (4)
(3(10)) 0011(2) 0,011 положительная (3)
(- 3(10)) 1100(2) 1,100 отрицательная (3)

 

Диапазон представимых чисел: -(2s-1-1)…(2s-1).

Положительный момент заключается в том, что при сложении обратных кодов чисел как беззнаковых чисел получаем обратный код суммы.

Отрицательный момент заключается в том, что существует два представления (0) и при выполнении операций сложения в обратном коде требуется коррекция суммы с помощью циклического переноса единицы переполнения из знаковых разрядов суммы.

3. Дополнительный код. Наиболее распространенный способ представления отрицательных целых чисел в компьютерных системах.

Он позволяет заменить операцию вычитания на операцию сложения, чем упрощает архитектуру компьютерной системы.

Дополнительный код является дополнением числа до некоторого граничного числа (|Xmax+1|=2s).

Дополнительный код положительного числа совпадает с прямым кодом.

Для получения дополнительного кода отрицательного числа существует три способа:

- все цифры модуля исходного числа заменяются на взаимно обратные, то есть производится инверсия всех цифр числа, затем к полученному значению добавляется единица в младшем разряде;

- из модуля числа вычитается (1) младший бит, а затем инвертируются все разряды;

- необходимо записать n-битный модуль числа. Затем просматривать число справа налево, сохранить все младшие нули и первую встретившуюся (1), а остальные биты инвертировать.

Дополнительный код числа определяется соотношением:

 

. (3.10)

 

. (3.11)

 

где - , C = Xгр. равняется весу не существующего в данном числе разряда, расположенного слева от знаковой цифры.

 

Отображение s-битных наборов ( дополнительный код верхняя числовая прямая) на числовую ось ( числа нижняя числовая прямая ) для компьютерной системы показано на рис. 3.5.

 

 

Рисунок 3.5 - Отображение s-битных наборов (дополнительный код ) на числовую ось

 

Например:

 

Десятичное число Двоичное число Дополнительный код Комментарии
(0(10)) 0000(2) 0,000 положительный (0)
(4(10)) 0100(2) 0,100 положительная (4)
(- 4(10)) 1100(2) 1,100 отрицательная (4)
(3(10)) 0011(2) 0,011 положительная (3)
(- 3(10)) 1101(2) 1,101 отрицательная (3)

 

Диапазон представимых чисел: -(2s-1)…(2s-1).

Свойства дополнительного кода:

- при сложении чисел в дополнительном коде как беззнаковых чисел получаем дополнительный код суммы. Знаковые биты суммируются обычным образом, а возникающий при их сложении перенос игнорируется.

- любое число в дополнительном коде можно считать младшими битами («хвостом») числа любой длины, если содержимое знакового бита копировать влево. Эта операция называется расширением знака. Используется, когда исходные операнды в операциях сложения и вычитания имеют разную длину.

Свойства кодов:

1. Операции должны выполняться над данными, представленными в одном и том же коде: ПК-ПК, ОК-ОК, ДК-ДК;

2. Положительные числа в ПК, ОК, ДК не меняют своего представления;

3. Результат выполнения операций сложения и вычитания над числами, представленными в ПК, ОК или ДК, являются ПК, ОК или ДК соответственно;

4. Двоичный набор, представляющий (-0) в ПК и ДК, является запрещенной комбинацией;

5. В отличие от ПК, в ОК и ДК нельзя отбрасывать нули после знакового разряда в целой части и нули в конце дробной части отрицательного числа (разрешается отбрасывать 1).

 

3.1 Арифметические флажки

 

Флажки являются признаками, представляющими общую характеристику результата выполнения операции. Наиболее широко применяются следующие флажки:

- флажок переноса (Flag Carry), обозначаемый (FC). Устанавливается в (1) в двух случаях:

1. Если при выполнении операции сложения имеет место перенос из старшего бита результата (представляет собой расширение результата на 1 бит влево);

2. Если при выполнении операции вычитания имеет место заем (borrow) в старший бит. Это возможно в случае, если уменьшаемое меньше вычитаемого. Если операнды интерпретируются как беззнаковые числа, данный флажок является признаком переполнения компьютерной системы.

В операциях над знаковыми числами самостоятельного значения не имеет.

- флажок вспомогательного переноса или дополнительный перенос (Flag Auxiliary), обозначаемый (FA). При сложении показывает перенос, а при вычитании - заем из младшей тетрады (бит 3) результата. Используется в операциях двоично-десятичной арифметики.

- флажок нуля (Flag Zero), обозначаемый (FZ). Признак нулевого результата. Устанавливается в (1) когда результат выполнения операции равняется (0).

- флажок знака (Flag Sign), обозначаемый (FS). Повторяет состояние знакового бита.

- флажок переполнения (Flag Overflow), обозначаемый (FО).

В операциях над знаковыми числами показывает, находится ли результат внутри диапазона представимых чисел:

- (FO) = 0 - результат правильный;

- (FO) = 1 - возникло переполнение. Следует отметить, что (FO) устанавливается в (1), если перенос в старший разряд и из него не совпадают.

 

3.2 Контроль переполнения в компьютерных системах

 

Возможно только при сложении чисел с одинаковыми знаками, когда для представления результата недостаточно отведенного количество разрядов (требуется больше, чем для представления операндов). Это может приводить не только к неправильному (по абсолютной величине) результату, но и к неправильному его знаку. Независимо от кода для представления отрицательных чисел (обратный или дополнительный) переполнение разрядной сетки имеет место всегда, если только при сложении положительных чисел возникает перенос в знаковый разряд, а при сложении отрицательных чисел такой перенос равен нулю. Введение масштабных коэффициентов, на которые необходимо умножить все исходные данные перед решением задачи, позволяет предотвратить переполнение. В компьютерных системах предусматривают специальные средства для обнаружения переполнения разрядной сетки:

- программный способ; основан на том, что при сложении чисел с одинаковыми знаками знак суммы должен совпадать со знаками операндов;

- аппаратный способ; основан на использовании модифицированных кодов.

При использовании модифицированных кодов знак числа изображается двумя одинаковыми цифрами. Эти цифры в процессе выполнения операций обрабатываются так же, как и числовые разряды. При этом появление в знаковых разрядах разных цифр (01 при сложении положительных и 10 при сложении отрицательных двоичных операндов) свидетельствует о переполнении разрядной сетки.

Модифицированный код позволяет формировать правильный знак результата даже при наличии переполнения.

Этот знак сохраняется во втором (старшем) знаковом разряде. Такой способ обнаружения переполнения разрядной сетки наиболее распространен в компьютерных системах, несмотря на некоторую избыточность в аппаратных средствах для представления чисел, поскольку позволяет оперативно (то есть, одновременно с результатом) получить информацию о переполнении.

На рис.3.6 представлен формат двоичного знакового числа с использованием модифицированного кода.

 

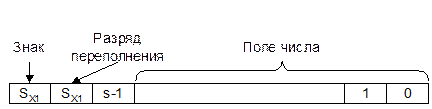
Рисунок 3.6 - Формат двоичного знакового числа с использованием модифицированного кода.

 

При выполнении операций сложения и вычитания чисел в дополнительных кодах обрабатывающее устройство компьютера не делает различий между знаковыми и беззнаковыми операндами.

То есть операнды должны интерпретироваться самим пользователем как знаковые или беззнаковые. В операции вычитания используется дополнительный код вычитаемого. Если длина операндов превышает длину машинного слова, то сложение и вычитание выполняют в несколько приемов, организуя программный цикл.

Операцию начинают с младших частей операндов, «продвигаясь» далее в сторону старших частей. На каждом шаге должны обрабатываться возникающие переносы (или заемы).