Рассмотрим частный случай
Сетей.
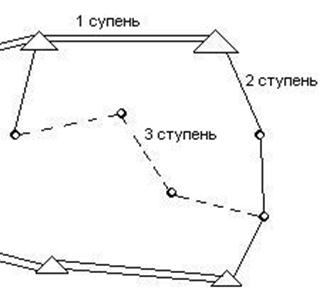 Наиболее слабый пункт будет находится в последней ступени. Наивысшая точность измерения в первой ступени.
Наиболее слабый пункт будет находится в последней ступени. Наивысшая точность измерения в первой ступени.
Введем следующие обозначения:
mi – ср.кв. ошибка ступени с номером i;
mi-1 – ср.кв. ошибка в положении наиболее слабого пункта в ступени i-1;
mизм – ср.кв. ошибка пункта i-той ступени, вызванная ошибками выполняемых в ней измерений.
Справедливым будет выражение m2i = k2m2i-1+m2изм. mu i = mизм.
k – некоторый коэф., который устанавливается на основе научных исследований.
m22 = k2m21+m2u2
mu2 – ср.кв. ошибка положения пункта, вызванная измерениями во второй ступени.
m23 = k2m22+m2u3 = k2(k2m21+m2u2)+m2u3 = k4m21+k2m2u2+m2u3
m24 = k2m23+m2u4 = k2(k4m21+k2m2u2+m2u3) + m2u4 = k6m21+k4m2u2+k2m2u3+m2u4
Настоящие выражение можно обобщить для n – ступеней:
m2n = k2n – 2m21 + k2n – 4m2u2 + k2n – 6m2u3 + k2n – 8m2u4 + … + m2un
Приведем подобные в данном выражении, сделав следующие допущения m2u1 = m2u2 = … = m2un = m2u
m2n = k2n – 2m21 + m2u(k2n – 4 + k2n – 6 + … + 1)
В скобках – сумма членов геометрической прогрессии, в которой
a1 = 1 – числитель
q = k2 – знаменатель.
В общем сумма членов геометрической прогрессии равна
S = a1(qn– 1)/(q-1)
S = 1(k2(n-1) – 1)/(k2 – 1)
И, соответственно, получим
m2n = k2n – 2m21 + m2u (k2(n - 1) – 1)/(k2 – 1)
Исходя из этого выражения можно, задаваясь mn , m1, k, mu, рассчитать значения n, т.е. число ступеней и наоборот при известном числе ступеней, задаваясь другими значениями, можно определить k, mu
Пусть опорная сеть развивается так

Мы имеем случай односторонней привязки, в этом случае К=1.
Это самый неблагоприятный случай, но расчеты при нем будут гарантированны для всех случаев практики.
При К стремящемуся к 1 найдем предел дроби:
(К^2(n-1) – 1)/(k²– 1) ; lim(k^2(n-1) – 1)/(k^2-1)
Мы получим неопределенность 0/0, для решения такой неопределенности применим правило Лопиталя, для этого продифференцируем числитель и знаменатель по К и найдем предел производных числителя и знаменателя, тогда будем иметь: lim(2(n-1)*k^(2(n-1)-1)/2k=n-1.
То есть в самом неблагоприятном случае имеем простое выражение
Mn^2= k^2(n-1) * m1^2 + mu^2 * (n-1)
Однако мы имеем двустороннюю привязку всегда, при этом значение К, будучи меньше единицы, меньше 0,5 не бывает.
Исследуем при каком значении n можно пренебречь ошибками исходных пунктов
Mn^2=0.5^2(n-1) * m1^2 + mu^2 * (n-1)
При n=2 0.5^2(n-1) =0.25,
при
n=3 0.5^2(n-1) =0.0625,
при
n=4 0.5^2(n-1) =0.0156
В технике принято, если одна из составляющих меньше другой в 10 раз, то ею можно пренебречь, Из этого следует, что ошибки исходных пунктов имеют существенное влияние лишь на 3-ю ступень развития опорной межевой сети. Другими словами при расчете точности геодезической сети следует учитывать ошибку лишь 2-х предыдущих ступеней.
§2. РАСЧЕТ ЧИСЛА И ТОЧНОСТИ СТУПЕНЕЙ ГЕОДЕЗИЧЕСКОЙ ОПОРЫ.
Для расчета числа и точности ступеней геодезической опоры воспользуемся формулой (9) самого неблагоприятного случая влияния исходных данных.
В соответствии с ней средняя квадратическая ошибка наиболее слабоопределяемой точки в последней ступени определяется выражением:
m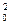 = m
= m + m
+ m + … + m
+ … + m  , (17)
, (17)
где mi = mn.
В предположении равенства между собой всех составляющих этого выражения получается формула (14).
Однако если принять, что
 (18)
(18)
для всех i, то можно записать что
 (19)
(19)

 (20)
(20)
Полагая, что m2 = km,
То 
Соответственно  (21)
(21)
В соответствии с (18) – (21) выражение (17) можно переписать так:
m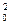 =
=  +
+  + … + m
+ … + m (22)
(22)
или
m = m
= m
 (23)
(23)
Находя в (23) общий знаменатель перепишем его так:
m = m
= m
 (24)
(24)
или
m =
=  (25)
(25)
Исходя из этого выражения можно находить mo, n, mn и k в отдельности при заданных других величинах.
Например, при определенном k, mn и mo можно вычислить n. Если задано mo, k, n, то можно вычислить mi.
Действительно исходя из (17)
m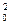 = m
= m + m
+ m + … + m
+ … + m + … + m
+ … + m (26)
(26)
Очевидно, что в соответствии с (21)




Тогда
m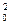 =
=  +
+  + … + m
+ … + m + … +
+ … +  (27)
(27)
Полагая в (27) общий знаменатель k запишем
запишем
m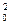 =
=  (28)
(28)
Следовательно
m =
= 
 (29)
(29)
или
m =
=  (30)
(30)
В заключении отметим следующее. Во всех предыдущих выводах оценивалось лишь влияние ошибок положения исходных пунктов. Однако кроме этого влияние имеет место еще влияние ошибок исходных дирекционных углов. В наиболее неблагоприятном случае ошибки исходных дирекционных углов увеличивают дисперсии определяемых пунктов в последующей ступени в 2 раза.
Следовательно, формулы (14), (12) и (13) можно записать так:
m = nm
= nm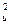 (2
(2 + 2
+ 2 + … + 1).
+ … + 1).
§3. МЕТОДИКА РАСЧЕТА ТОЧНОСТИ ПРОЕКТА ГЕОДЕЗИЧЕСКОЙ СЕТИ.