Примеры.
1. Написать уравнение пучка прямых, проходящих через точку 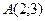 . Выбрать из этого пучка прямые, составляющие с осью Ох углы:
. Выбрать из этого пучка прямые, составляющие с осью Ох углы:
а) 45°; б) 60°.
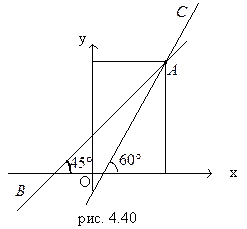 Решение. Запишем уравнение пучка прямых с центром в точке
Решение. Запишем уравнение пучка прямых с центром в точке 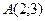
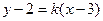
а) для прямой (АВ) угловой коэффициент 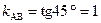
б) для прямой (АС) 
уравнение прямой (АВ) 
уравнение прямой (АС) 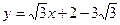
2. В треугольнике с вершинами А(−2;0); В(2;6) и С(4;2). Найти уравнения высоты, проведенной из вершины В, и медианы, проведенной из вершины В.
Решение.  ;
;  .
.
 а) уравнение BD будет искать как прямую, проходящую через данную точку В(2;6), тогда ее уравнение
а) уравнение BD будет искать как прямую, проходящую через данную точку В(2;6), тогда ее уравнение 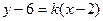 , так как
, так как  , то угловые коэффициенты этих прямых удовлетворяют условию
, то угловые коэффициенты этих прямых удовлетворяют условию 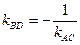 .
.
Угловой коэффициент АС найдем по двум точкам 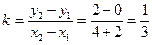 , тогда
, тогда 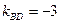
Уравнение высоты (ВD): 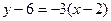 , или
, или 
б) Чтобы найти уравнение медианы (ВЕ) найдем координаты точки Е, являющейся серединой отрезка АС.
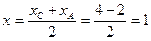 ;
; 
Используя уравнение прямой, проходящей через две точки: В(2;6)и Е(1;1)
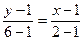 ;
; 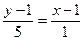 , откуда получается ее уравнение медианы (ВЕ):
, откуда получается ее уравнение медианы (ВЕ): 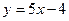
Функция у=|х|.
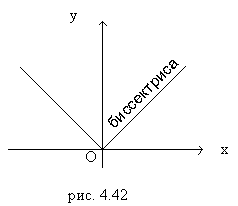
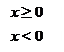 По определению
По определению 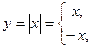
Функция задается двумя различными аналитическими выражениями.